TDT4120 Algoritmer og datastrukturer

Dette er et selvskrevet kompendium i TDT4120 ved NTNU. Kompendiet er strukturert etter læremålene i pensumheftet 2020.

Kompendiet er ikke komplett og definitivt ikke perfekt, så gjerne bidra!

Overordnede læringsmål i faget

Ha kunnskap om
- et bredt spekter av etablerte algoritmer og datastruktuer
- klassiske algoritmiske problemer med kjente effektive løsninger
- komplekse algoritmer uten kjente effektive løsninger
Ha ferdigheter for å
- analysere algoritmers korrekthet og kjøretid
- formulere problemer som kan løses av algoritmer
- konstruere nye effektive algoritmer
Være i stand til å
- bruke eksisterende algoritmer og programvare på nye problemer
- utvikle nye løsninger på praktiske algoritmiske problemstillinger
Ved hver algoritme skal man
- kjenne til den formelle definisjonen av det generelle problemet algoritmen løser
- kjenne til eventuelle tilleggskrav den stiller for å være korrekt
- vite hvordan den oppfører seg, kunne utføre den, trinn for trinn
- forstå korrekthetsbeviset; hvordan og hvorfor virker det egentlig?
- kjenne til eventuelle styrker og svakheter sammenlignet med andre
- kjenne til kjøretiden under ulike omstendigheter, og forstå utregningen
Ved hver datastruktur skal man
- forstå algoritmene for de ulike operasjonene på strukturen
- forstå hvordan strukturen representeres i minnet
Ved hvert problem skal man kunne
- angi presist hva input er
- angi presist hva output er og hvilke egenskaper det må ha

Problemer og algoritmer

Brute force er ofte helt ubrukelig. Dekomponer til mindre instanser og bruk de til å finne en løsning.

En algoritme er en tydelig definert fremgangsmåte som kan ta en verdi eller en mengde verdier som input og produserer en verdi eller en mengde verdier som output. Algoritmen er ofte en sekvens av beregninger, presist beskrevet. Input verdiene kan deles opp i flere instanser.

Å analysere en algoritme har betydningen å "forutse ressurskravene til algoritmen": minne, kommunikasjonsbåndbredde, hardware, beregningstid, og ofte totalkostnaden av disse, i tillegg til å vise korrekthet.

Random-access machine modellen (RAM)

I dette faget bruker vi en abstrakt maskin som har følgende egenskaper:

Aritmetikk: $+$ $-$ $*$ $/$ $\bmod$, $\lfloor x \rfloor$, $\lceil x \rceil$ (enkle instruksjoner)
Flytting av data og programkontroll
Instruksjoner kjøres sekvensielt og ikke parallelt
Håndterer heltall og flyttall

Alle disse operasjonene tar konstant tid. Maskinen modellerer ikke minnehierarki og caches, og den kan dermed ikke modellere parallell utførelse.

Kjøretid

Et mål på effektiviteten til algoritmen er det viktigste når man skal analysere alle algoritmer. Vi trenger å beregne kjøretider fordi vi har en begrensning på hvor raskt vi kan løse problemer og hvor mye lagringsplass en datamaskin har tilgjengelig. Kjøretiden er det asymptotiske forholdet mellom størrelsen på problemet og hvor lang tid det vil ta å løse det.

Problem: Relasjon mellom input og output
Instans: En bestemt input
Problemstørrelse, $n$: Lagringsplass som trengs for en instans
Kjøretid: En funksjon av problemstørrelsen; større problemer krever mer tid (men hvor mye?)
Eksempel: Hvis vi teller operasjoner, og hver operasjon tar ett mikrosekund, hvor mye rekker vi på ett år?

Vi er interessert i hvor fort kjøretiden vokser. Vi er interessert i en grov størrelsesorden.

Vanlige kjøretider rangert i synkende rekkefølge

Kompleksitet	Navn	Type
$\Theta(n!)$	Factorial	Generell
$\Omega(k^n)$	Eksponensiell	Generell
$O(n^k)$	Polynomisk	Generell
$\Theta(n^3)$	Kubisk	Tilfelle av polynomisk
$\Theta(n^2)$	Kvadratisk	Tilfelle av polynomisk
$\Theta(n\lg n)$	Loglineær	Kombinasjon av lineær og logaritmisk
$\Theta(n)$	Lineær	Generell
$\Theta(\lg n)$	Logaritmisk	Generell
$\Theta(1)$	Konstant	Generell

Den gjennomsnittlige kjøretiden til en algoritme er kjøretiden man i gjennomsnitt vil få ved et tilfeldig input. Den kan indirekte si noe om at verste tilfelle ikke er bedre og beste tilfelle ikke er verre.

Asymptotisk notasjon

Asymptotiske notasjon beskriver hvordan en funksjon oppfører seg når inputstørrelsen blir veldig stor (tenk grenseverdier og summer). I algoritmesammenheng er funksjonen ofte tidsbruk gitt en inputstørrelse.

Big-O Cheat Sheet er bra for å visualisere asymptotisk notasjon.

Asymptotisk notiasjon gir oss ikke en presis beskrivelse av veksten til en funksjon, men den gir oss øvre og nedre grenser. Det gjør det enklere å beskrive og sammenligne ulike algoritmer.

Dropp konstanter og lavere ordens ledd
Notasjonen tilsvarer og kalles:
- $\omega$ $\leftrightarrow$ $>$ (lille omega)
- $\Omega$ $\leftrightarrow$ $\ge$ (store omega, nedre grense)
- $\Theta$ $\leftrightarrow$ $=$ (store theta, øvre og nedre grense)
- $O$ $\leftrightarrow$ $\le$ (store o, øvre grense)
- $o$ $\leftrightarrow$ $<$ (lille o)

Asymptotisk optimal

Den asymtotiske optimale kjøretiden = den beste mulige kjøretiden for det gitte problemet. Vanligvis verste tilfelle, men kan variere.

«Optimal» betyr «best» (altså det du kaller «mest optimal»). Om man vil ha mange aktiviteter, så vil de optimale løsningene være de løsningene som har flest aktiviteter. Ingen andre vil være bedre, men det kan være flere optimale løsninger (som altså har nøyaktig like mange aktiviteter/som er nøyaktig like bra).

En optimal løsning er så bra som det er mulig å være – ingen løsninger kan være bedre – men det kan være flere optimale løsninger, som er nøyaktig like bra.

F.eks. sier vi at Merge sort er asymptotisk optimal, fordi den har verste kjøretid $O(n\lg n)$, og vi vet at verste kjøretid for sortering generelt er $\Omega(n\lg n)$. Dermed går det ikke an å bli bedre i verste tilfelle. Men i beste tilfelle er jo f.eks. Insertion sort bedre, så den har en asymptotisk optimal best-case (som ofte ikke er så interessant; det er jo lett å legge til en optimal best-case, f.eks. ved å bare sjekke om input allerede er sortert før vi setter igang sorteringen).

Referanser: Piazza H20 @158, Piazza H20 @240

Forenkling av asymptotisk notasjon

Grunnen til at man forenkler asymptotisk notasjon er at ikke alle beskrivelser er like presise. Noen deler av et uttrykk er altså så upresis at man kan fjerne dem helt uten at det påvirker den faktiske kjøretiden. Dette er nyttig når man har store, uoversiktlige uttrykk som man ønsker å forenkle uten tap av presisjon.

Uttrykk $B$ er en forenkling av uttrykk $A$ dersom $A=B$ og $B$ er enklere enn $A$
Medføre minst mulig tap av presisjon; Høyre side må ikke utelukke noen alternativer på venstre side.

Generelt er ideen at et uttrykk $B$ er en forenkling av uttrykk $A$ dersom $A=B$ og $B$ er enklere enn $A$. Forenkling bør medføre minst mulig tap av presisjon. Med enklere menes kortere/færre tegn eller lignende. I asymptotisk notasjon er sum det samme som maksimum, og man må velge uttrykk til høyre som ikke har strengere øvre og/eller nedre grenser enn venstresiden. Summer som inneholder et ledd med kun en nedre grense kan ikke ha noen øvre grense totalt sett. Ledd som blir beskrevet kun med nedre grense f.eks. $\Omega(n)$ kan ha en ukjent øvre grense. Denne ukjente øvre grensen kan være uendelig stor. Vi må ha dette i bakhodet når vi skal forenkle sammensatte uttrykk.

Forenkling eksempel 1

$$O(n) + \Omega(n) = \Omega(n)$$

Uansett hvilken funksjon vi har fra $O(n)$ og $\Omega(n)$, om vi legger dem sammen vil den resulterende funksjonen tilhøre klassen $\Omega(n)$. Det vil ikke påvirke resultatet å legge til flere øvre grenser $O(anything)$.

Uformelt kan man si "Funksjonen er minst $n$". Da kan man like gjerne si "Funksjonen er minst $n$ pluss maks $n^2$". Det endrer ingenting. Det blir som om vi sier «Emnet har minst 1000 studenter og så maks 200 studenter til». Det eneste vi vet da er at det er minst 1000 studenter. Og vi kan like gjerne uttrykke det som «Emnet har minst 1000 studenter og så maks 2.000.000 studenter til». Det er fortsatt korrekt. Vi vet fortsatt bare at emnet har minst 1000 studenter. (Piazza H20 @21)

Forenkling eksempel 2

$$\Theta(n^2) + O(n^4) + \Omega(\log n) = \Omega(n^2)$$

$\Omega(n^2)$ vil være en mer generell notasjon og derfor OK. $\omega(n^2)$ vil være feil fordi lille omega er en strengere notasjon, og utelukker leddet som inneholder $\Theta(n^2)$.

Klasser av input

Best, verst og forventet
Kjøretid: Funksjon av problemstørrelse
Best-case: Beste mulige kjøretid for en gitt størrelse
Average-case: Forventet, gitt en sannsynlighetsfordeling. Har vi ingen sannsynlighetsfordeling antas alle inputs like sannsynlige.
Worst-case: Verste mulige (brukes mest)

Dekomponering/rekursiv dekomponering

Eks: summere elementene i en tabell
Rekursjon: summer alle unntatt siste - en funksjon kaller seg selv
Grunntilfelle: tom sum er null
Induktivt premiss: summen er rett
Induksjonstrinn: legg til siste element

Induksjon

Del opp i mindre problemer (trinn for trinn)
Induktivt premiss: anta at du kan løse de mindre problemene
Induksjonstrinn: konstruer fullstendig løsning ut fra delløsningene

Eksempel:

Velge vilkårlig heltall å vise for det, da kan det vises for alle
Midlertidig anta $P$ og vis deretter $Q$ - da kan $P$ implisere $Q$

Tolkning: Hva er relasjonen mellom input og output?
Analyse: Del en vilkårlig instans i delinstanser
Syntese: Bygg løsning av hypotetiske delløsninger

Iterativ dekomponering: Induksjon - Iterativ utgave

(Løkke) Invariant: egenskap som ikke endres. Sann før og etter hver iterasjon
- Initialize: anta at invariant er sann før start
- Vedlikehold: holder den før/etter interasjon?
- Terminering: løkken sier noe nyttig
Vedlikehold i hver iterasjon

Insertion sort

Link til insertion sort

Datastrukturer

For å unngå grunnleggende kjøretidsfeller er det viktig å kunne organisere og strukturere data fornuftig. En datastruktur er en måte å organisere og strukturere data på for å muliggjøre tilgang og modifikasjon. Det er ingen universal datastruktur som fungerer godt for alle formål. Det er derfor viktig å betrakte egenskapene til datastrukturen du trenger for å løse problemet ditt.

Stakker og køer (stacks and queues)

Stakker og køer er dynamiske sett med 2 viktige metoder, PUSH og POP, som hhv. legger til og fjerner elementer.

En stack har en "Last In First Out" (LIFO) struktur. En stakk er som en stabel med tallerkener. Man kan kun legge til og fjerne elementer på toppen. For å nå bunnen må man først fjerne alt på toppen. POP returnerer elementet som sist ble satt inn.

class Stack:
     def __init__(self):
         self.l = []

     def isEmpty(self):
         return self.l == []

     def push(self, item):
         self.l.append(item)

     def pop(self):
         return self.l.pop()

En kø har en "First In First Out" (FIFO) struktur. POP eller DEQUEUE returnerer elementet som først ble satt inn med $O(1)$.

class Queue:
    def __init__(self):
        self.l = []

    def isEmpty(self):
        return self.l == []

    def enqueue(self, item):
        self.l.insert(0,item)

    def dequeue(self):
        return self.l.pop()

Prioritetskø

En prioritetskø er en type kø som ikke er "First In First Out" (FIFO) strukturert. Alle elementer i køen har en verdi som angir prioritet, og det er alltid elementet med størst eller minst som først tas ut av køen.

DEQUEUE vil ta ut elementet med størst/minst prioritet
ENQUEUE vil sette inn et element med en gitt prioritet

Lenkede lister

En lenket liste er en lineær datastruktur som representerer elementer i sekvens. Hvert element i lista er en node med en verdi og en peker som peker videre på det neste elementet. I en dobbel-lenket liste peker også hver node/element på det forrige elementet.

En node er et datapunkt i en datastruktur som inneholder data.

Sentinels: NIL-objekter. Et dummy objekt som brukes for å lage avgrensninger, for eksempel i enden av en liste.

LIST-SEARCH(L, k)
1   x = L.head
2   while x =/= NIL and x.key =/= k
3       x = x.next
4   return x

LIST-SEARCH'(L, k)
1   x = L.nil.next
2   while x =/= L.nil and x.key =/= k
3       x = x.next
4   return x

NB! Vær bevisst på parameterne metodene får inn. Dersom det er en key (en verdi) vil kjøretiden i dobbelt-lenket lister være $\Theta(n)$ for List-Delete. Dersom du får inn en node som parameter vil kjøretiden være $O(1)$.

Det finnes varianter av metodene som innebærer disse NIL-objektene. De kan forbedre kjøretiden og gjøre koden mer lesbar, men gir mer overhead.

Handling	Enkel-lenket liste	Dobbel-lenket liste
Innsetting på starten	$O(1)$	$O(1)$
Innsetting på slutten	$O(n)$	$O(1)$
`List-Insert`	$O(n)$	$O(n)$
`List-Search`	$O(n)$	$O(n)$
`List-Delete`	`List-Search` $+\ O(1) = O(n)$	$O(1)$

I en dobbel lenket liste gjøres innsetting på $O(1)$ da man kun trenger å endre .prev og .next til de nye naboene.

Enkel-lenkede lister kan ikke søke baklengs gjennom listen. Det betyr at for å sette inn et element på slutten av en liste, så må den bla seg gjennom fra første til siste element, derav $O(n)$. En dobbelt lenket liste kan bruke .prev til dette og får dermed kjøretiden $O(1)$ for samme operasjon.

Pekere og objekter

En peker peker til en minneadresse. På den minneadressen kan det være et objekt. Objekter kan ha pekere som peker til forskjellige minneadresser. Disse kan implementeres i form av lenkede lister.

Objekter kan bli representert av flere arrays eller kun et array:

I en multiple-array situasjon vil de forskjellige arrayene tolkes som for eksempel elementer, pekere fram og tilbake, og $\backslash$ for NIL.
I en enkel array vil posisjonen til elementene relativt til hverandre indikere hvordan objektet skal representeres (igjen med pekere fram og tilbake).

Eksempel på et objekt representert av en enkel array

Dette er nyttig for en datamaskin når den f.eks. ønsker å sortere en array. Isteden for å faktisk flytte på alle objektene kan den endre på pekerne til å peke i sortert rekkefølge.

Hashtabeller

Hashtabeller bruker en kombinasjon av tabeller, addressering og hashing (koding) til å lagre lokasjoner av data.

En enkel måte å si det på er at den lagrer data på en lokasjon og gir den en nøkkel. Nøkkelen hasher den til å bli en unik kode som referer tilbake til den unike lokasjonen. Målet med dette er å fordele dataen jevnt over alle minnelokasjonene i tabellen og å kunne hente dem tilbake raskt.

Bruksområde: I stedet for å lete gjennom en liste, som kan ta $O(n)$ i verste fall, eller en sortert liste på $O(\log n)$, vil letetiden i en hashtabell være konstant, $O(1)$, fordi lagerstedet til en hashtabell vanligvis er i maskinens hurtigminne hvor man har $O(1)$ tilgang til alle plassene.

Begreper:

Direkte adressering: Du henter ut data direkte på $O(1)$. F.eks. ved å bruke nøkler (keys) for å hente ut data.
Nøkkel = indeks: Du gir en nøkkel for henting av data.
Hashing: Vi får inn en nøkkel og knøvler den så den blir en lovlig nøkkel. Knøvlingen $\rightarrow$ Hashing, den hakkes opp. En lovlig nøkkel er det som er tillat av hashfunksjonen.

Kollisjoner

Hvis en hashfunksjon gir samme lovlige nøkkel ved samme input. Blir verdiene satt i samme plass i minnet og det oppstår en kollisjon. Dette kan man løse med f.eks. chaining.

Chaining - en teknikk for å løse kollisjoner

Chaining vil si at man legger elementer i en lenket liste på samme nøkkel. Dersom man har en skikkelig dårlig hashfunksjon vil mange elementer ende på samme nøkkel. Det vil medføre verre kjøretid fordi man ikke kan hente ut verdien på konstant tid, men må traversere listen i tillegg (Ref: List-Search med key som parameter). Vi ønsker hashfunksjoner som gir en jevn distribusjon av nøkler uansett input.

Kjøretiden for de ulike operasjonene Chained-Hash-Insert, Chained-Hash-Search og Chained-Hash-Delete vil variere fra hvilken datastruktur som brukes i chainingen. Det kan f.eks. være gunstig å bruke en dobbelt-lenket liste, men vær obs på hva som tas inn som parametere i metodene for å beregne kjøretid (key vs node).

En annen løsning for å løse kollisjoner er å putte verdiene andre steder i tabellen (utenfor pensum).

Grunnleggende hashfunksjoner

Et krav for en hashfunksjon er at den må være deterministisk: Den må alltid gi samme output for samme input.

$$h(k) = \lfloor km \rfloor, 0 \leq k < 1$$ $$h(k) = k \space mod \space m$$ $$h(k) = \lfloor m (kA \space mod \space 1) \rfloor, 0 < A < 1$$

Hva karakteriserer en god hashfunksjon?

Den skal fordele input så jevnt utover hele hashtabellen på en måte som virker uniformt tilfeldig.
Dersom det er et homogent input, det er systematikk og mønster i input skal det ikke oppstå kollisjoner.

Statiske datasett

Når man har statiske datasett kan man lage en skreddersydd hashfunksjon. Dette medfører at man kan garantere worst-case $O(1)$ fordi man alt vet hva som skal inn i tabellen.

Amortisert analyse

Amortisert analyse er en metode for å kunne analysere en gitt algoritmes kompleksitet.

It gives the average performance (over time) of each operation in the worst-case.

Kjøretid for en enkeloperasjon: ikke alltid informativt
Se på gjennomsnitt per operasjon etter mange har blitt utført. Dersom det er noen få "kostbare" operasjoner vil gjennomsnittet fortsatt bli lavt når man ser på helheten.

Amortisert analyse ser på gjennomsnittet av worst case tilfellene ved forskjellige inputstørrelser, som i mange tilfeller er mye bedre enn det verste tilfellet. Det er derfor worst case ofte er mer pessimistisk enn amortisert analyse.

Når du har en sekvens med operasjoner, som du kjenner kjøretiden til, så kan man utføre amortisert analyse.

Summen av toerpotenser (husk denne):

$$\sum^{h-1}_{i=0}2^i = 2^h-1$$

Ved bruk av summen av toerpotenser kan man regne ut den amortiserte kjøretiden for en algoritme som bruker f.eks. fordoblet allokering av plass.

Dynamiske tabeller

Som nevnt i amortisert analyse ønsker vi å allokere minne sjeldent fordi det tar lineær tid å allokere nytt minne og kopiere elementer. Vi velger med dynamiske tabeller å heller allokere mye minne av gangen når det blir behov.

Med amortisert arbeid blir kjøretiden akseptabel. Man øker størrelsen med en viss prosent. I eksempelet under øker den med x2 hver gang.

TABLE-INSERT(T,x)
1     if T.size == 0
2       allocate T.table with 1 slot
3       T.size = 1
4     if T.num == T.size
5       allocate new-table with 2*T.size slots
6       insert all items in T.table into new-table
7       free T.table
8       T.table = new-table
9       T.size = 2*T.size
10    insert x into T.table
11    T.num = T.num+1

Splitt og hersk

Splitt problemet inn i delproblemer som er mindre instanser av originalproblemet.
Hersk over delproblemene ved å løse dem rekursivt, eller hvis de er små nok løs delproblemene direkte.
Kombiner løsningene til delproblemene til en løsning for originalproblemet.

Maximum subarray problemet

Quick sort er in-place.

Rekurrenser

En type likning - Rekursive likninger
Eksempel på en rekurrens: $T(n)=4T(^n/_2) + n^2$

De beskriver f.eks. kjøretiden til rekursive algoritmer. Man trenger ikke bruke rekurrenser om det ikke er rekursjon!

Metoder for å regne ut rekurrenser:

Substitusjon
- Bytte ut inputargumenter til noe som gjør rekurrensen enklere å løse.
Rekursjonstre
Masterteoremet
- Rekurrensen må være på formen $T(n)=aT(^n/_b) + f(n)$
Iterasjonsmetoden (induksjon)
- Gjentatt ekspandering av den rekursive forekomsten av funksjonen - det gir oss en sum som vi kan regne ut
- Gjør at vi kan "se" et mønster
Variabelskifte

Substitusjon

Substutisjon innebærer mye manipulering av algebrauttrykk for å oppnå det man vil.

Gjett en løsning.
Anta at det holder for alle $m < n$.
Sett inn og substituer
Vis at det holder for ett grunntilfelle for en vilkårlig valgt $n$

Rekursjonstre

Iterasjonsmetoden med flere grener. Tegn ut hvert kall som noder i ett tre. Fin måte å visualisere arbeidet, men kan være overveldende i starten.

Vi itererer gjennom hva algoritmen koster for hvert nivå i treet, og legger det sammen. Da får vi en sum (kostnad løvnivå + $\sum_{h-1}^{i=0}$ pris for nivå $i$).
Høyden til treet, er hvor lang tid det tar å komme seg til grunntilfellet. Kjøretiden blir kostnaden til hvert nivå.
Kan ofte bruke masterteoremet istedet, men det bevises via rekurrenstrær.
Eks: $T(n)=3T(n/4)+cn^2=3T(n/4)+\Theta(n^2)$. (s. 88 i boka)

Masterteoremet

Kontekst: Finne kjøretid, ofte for splitt og hersk algoritmer

Dekker mange tilfeller av rekursiv dekomponering. Krever at betingelsene følges nøyaktig.

$$T(n) = aT(^n/_b) + f(n)$$ $$a \ge 1,\ b > 1$$

Identifiser $a, b, f(n)$
Regn ut $\log_b(a) = d$ og finn graden av $f(n) = c$
Vurder forholdet mellom $c$ og $d$. Hvis $d>c$ gjelder tilfelle 1 med $O$. Hvis $c=d$ gjelder tilfelle 2 med $\Theta$. Hvis $d < c$ gjelder tilfelle 3 med $\Omega$.
Konsulter tabellen under med tilfeller

Tilfelle	Krav	Løsning
1	$f(n)\in O(n^{\log_b a-\epsilon})$	$T(n) \in \Theta(n^{\log_b a})$
2	$f(n)\in \Theta(n^{\log_b a} \log^k n)$	$T(n) \in \Theta(n^{\log_b a}\log n)$
3	$f(n)\in \Omega(n^{\log_b a+\epsilon})$	$T(n) \in \Theta(f(n))$

Fallgruve: Det holder ikke at arbeidet $f(n)$ i rotnoden av rekurrenstreet vokser større enn arbeidet $n^{\log_b(a)}$ i løvnodene. $f(n)$ må være større med polynomisk faktor.

Eksempel masterteorem 1

$$T(n)=64\cdot T(n/4)+3n^3+7n$$

$a = 64$, $b=4$, $f(n)=3n^3+7n$
$\log_4(64) = 3 = d$
Finn graden av $f(n)$ som her er $3=c$.
I vårt tilfelle er $d=c$ og dermed er det tilfelle 2 med $\Theta$.
Hvordan vi da finner løsningen baserer seg på tilfellet. Formatet på kjøretiden vår kommer dermed til å være på formatet til løsningen på tilfelle 2.

$$T(n) \in \Theta(n^{\log_b a}\log^{k+1}(n))$$ $$T(n) \in \Theta(n^{\log_4 64}\log^{0+1}(n))$$ $$T(n) \in \Theta(n^{3}\log^{}(n))$$

Eksempel masterteorem 2

def FUNCTION-A(n):
  FUNCTION-C(n)
  if n > 1:
    FUNCTION-A(n/3)
    FUNCTION-B(n-2)

def FUNCTION-B(n):
  FUNCTION-C(n)
  if n > 1:
    FUNCTION-A(n/3)

Funksjonen FUNCTION-C har kjøretid $\Theta(\sqrt(n))$. Hva blir kjøretiden til funksjonen FUNCTION-A, som funksjon av $n$?

Vi gjenkjenner rekurrensen på følgende måte:

Prøv å formulere funksjon A som en rekurrens ved å vurdere en operasjon av gangen:
- FUNCTION-C(n): Legg til FUNCTION-C(n)
- if n > 1: If-statements med en sjekk anses som ett steg.
- FUNCTION-A(n/3): For rekursive kall, i dette tilfellet der funksjon A kaller seg selv, vil vi sette inn $T_a(n/3)$.
- FUNCTION-B(n-2): Hva med parameteren $n-2$? Dette er en konstant endring og trenger dermed ikke å vurderes her. Sett inn funksjon C og A for B.
Dette gir oss: $$T_A(n) = T_C(n)+1+T_A(n/3)+T_C(n)+1+T_A(n/3)$$

Bytt så ut $T_C(n) = \Theta(\sqrt(n))$

$$T_A(n) = \sqrt(n)+1+T_A(n/3)+\sqrt(n)+1+T_A(n/3)$$

$$T_A(n) = 2\cdot T_A(n/3)+2\cdot \sqrt(n)+2$$
Bruk deretter masterteoremet:
- $a = 2$, $b=3$, $f(n)=2\cdot \sqrt(n)+2$
- $\log_3(2) \approx 0.95 = d$
- Finn graden av $f(n)$ som her er $1/2=c$. Merk: $\sqrt{n} = n^{1/2}$
- Vurder forholdet mellom $c$ og $d$. Her er $d>c$ og dermed er det Masterteorem-tilfelle 1 med $\Omega$.
- Hvordan vi da finner løsningen baserer seg på tilfellet. Formatet på kjøretiden vår kommer dermed til å være på formatet til løsningen på tilfelle 2.

Dette gir oss følgende

$$T(n) \in \Theta(n^{\log_b a})$$ $$T(n) \in \Theta(n^{\log_3 2})$$

Iterasjonsmetoden

Ta et rekursivt uttrykk, for eksempel
$$T(n) = T(n/2) + 1$$ $$T(1) = 1$$

Utvid opp i iterasjoner $$T(n) = T(n/2) + 1 = T(n/4) + 2 = T(n/2^i) + i$$

Vi ønsker nå å få argumentet $T$ lik $1$ for å få grunntilfellet. $$n/i^2 = 1 => i^2 = n => i = lg(n)$$ $$T(n) = T(1) + lg(n) = 1 + lg(n)$$

Variabelskifte

Bytt ut vanskelige uttrykk

Sett opp ny rekurrens av en annen variabel, f.eks. $T(n)=T(2^k)=S(k)$
Løs den, f.eks. med masterteoremet
Bytt tilbake til $T(n)$

Eksempel: Løs rekurrensen $T(n) = T(\sqrt{n})+\lg n$.

Rangering i lineær tid

Vi kan ofte få bedre løsninger ved å styrke kravene til input eller ved å svekke kravene til output. Sortering basert på sammenligninger ($x\leq y$) er et klassisk eksempel: I verste tilfelle må vi bruke $\lg n!$ sammenligninger, men om vi antar mer om elementene eller bare sorterer noen av dem så kan vi gjøre det bedre.

Worst case for sammenligningsbasert sortering (sorteringsgrensen)

Enhver sammenligningsbasert algoritme krever $\Omega(n\lg n)$ sammenligninger i worst-case.

Vi må vise at høyden til valgtreet er $n\lg n$. Vi har et valgtre med høyde $h$ og antall blader $l$ som kan nås fra roten. Da det er $n!$ permutasjoner som skal representeres av blad og et binært tre av høyde $h$ kan ikke ha mer enn $2^h$ blad, vil $n! \leq l \leq 2^h$, slik at $n! \leq 2^h$. Ved å ta logaritmen finner vi:

$$h\geq \lg(n!) = \Omega(n \lg n)$$

hvor $\lg(n!) = \Theta(n\lg n)$.

Det er umulig å sortere raskere uten å anta egenskaper ved problemet. Dette gjør at heap sort og merge sort er asymptotiske optimale sammenligningsbaserte sorteringsalgoritmer da de har en øvre grense på $O(n\lg n)$, det samme som den nedre grensen for sorteringsalgoritmer.

Stabile sorteringsalgoritmer

En sorteringsalgoritme kan sies å være stabil om rekkefølgen av like elementer i listen blir bevart etter sortering. For eksempel om vi har lista

$$[B1, C2, C1, A1]$$

og sorterer den kun etter bokstaver, vil rekkefølgen for $C$ forbli uforandret:

$$[A1, B1, C2, C1]$$

Vi sier ofte at den relative rekkefølgen opprettholdes.

Counting sort

Link til counting sort

Counting sort er en ikke-sammenligningsbasert sorteringsalgoritme som sorterer effektivt om det er mange like elementer i en liste.

Counting sort slår radix sort hvis antallet elementer $n \gg k$ forskjellige elementer.

Radix sort

Link til radix sort

Radix sort er en stabil ikke-sammenligningsbasert sorteringsalgoritme som sorterer elementer basert på siffer. Radix sort slår counting sort hvis antallet elementer $n \ll k$ forskjellige elementer.

Bucket sort

Link til bucket sort

Bucket sort er en ikke-sammenligningsbasert sorteringsalgoritme som krever uniform sannsynlighetsfordeling. Den deler og flytter elementene inn i like store intervaller/bøtter, og sorterter internt i bøttene med en annen sorteringsalgoritme.

Randomized-Select og Select

Rotfaste trestrukturer

Rotfaste trær gjenspeiler rekursiv dekomponering. I binære søketrær er alt i venstre deltre mindre enn rota, mens alt i høyre deltre er større, og det gjelder rekursivt for alle deltrær! Hauger er enklere: Alt er mindre enn rota. Det begrenser funksjonaliteten, men gjør dem billigere å bygge og balansere.

Et tre er en begrenset form av en graf. Trær har en retning (forelder-/barn-forhold) og inneholder ikke kretser/sykler.

Kjøretidsoversikt:

Terminologi

Indekseringen av elementer går fra topp-til-bunn, fra venstre til høyre. Det betyr at topp-elementet alltid har indeks 0, mens det mest høyrestående elementet på det laveste nivået har høyest indeks.

Det øverste elementet (med index 0) er rot-noden.
De midterste elementene (som har både foreldre og barn) regnes som interne noder.
De mest dyptstående elementene er løvnoder (leafs). De har ingen barn.

Når man snakker om trær er det vanlig å bruke terminologi som beskriver avstanden fra roten:

Avstanden mellom roten og et vilkårlig element kalles dybde.
Avstanden mellom roten og det dypeste elementet kalles høyden.

Heaps

En haug (heap) er en sortert tre-struktur. Elementer som legges til en heap blir først sammenlignet med sin forelder-node (parent). Avhengig av om haugen sorterer etter min eller max, blir verdiene byttet om i stien opp til roten helt til rekken er sortert.

Operasjoner på Heaps

Insert = $O(\log n)$
Fordi man må søke gjennom treet. Ettersom treet er $\log n$-høyt, må dette nødvendigvis bli kjøretiden.* En forenklet versjon i en tre-struktur heter TREE-INSERT med kjøretid $O(h)$.

Delete = $O(\log n)$
Av samme grunn som insert. En forenklet versjon i en tre-struktur heter TREE-DELETE med kjøretid $O(h)$.

Build = $O(n)$
Build bygger en heap uten å ta hensyn til sortering. Det vil si at den bare legger til legger til elementer i en trestruktur. Derfor er kjøretiden lineær.

Max-heapify = $O(\log n)$
Max-heapify tar input-elementene og konstruerer en Max-heap. Den sorterer nodene fra bunn til topp. Dermed er den bundet av høyden til heapen som er $\log n$.

Build-max-heap = Linear time
Build-max-heap bygger en heap ved å kjøre max-heapify på hver node den legger til. Max-heapify tar $O(\log n)$ tid, men ettersom Build tar lineær tid, overskirver denne Max-heapify. Altså får vi lineær tid.

Heapsort = $O(n \log (n))$
Heapsort bygger først en max-heap ved hjelp av Build-max-heap. Nå er det største elementet på toppen. Dette elementet hentes ut fra heapen. Den flytter så en av de minste elementene helt til toppen før den kjører Max-heapify igjen. Max-heapify garanterer at det største elementet i heapen nok en gang kommer til toppen. Denne prosessen gjør det mulig å hente ut det største elementet i heapen hver gang.*
$O(n \log (n))$ kommer av at det kjøres Max-heapify for hvert element.

Max-heap-insert, heap-extract-max, Heap-increase-key, Heap-maximum = $O(\log (n))$

En haug er komplett dersom alle interne noder har to barn og alle løvnoder er på samme nivå. Om antallet noder er $2^h-1$, for en eller annen høyde $h$, så er treet som haugen representerer komplett.

Bildet under illustrerer sorteringsprosessen etter at et element blir lagt til i haugen.

Den originale haugen
Element legges til
Elementet bytter plass med forelder-noden

Heap sort

Link til heap sort

Implementasjon av rotfaste trær

Rotfaste trær er basisvarianten av f.eks heaps og binære søketrær. Et tre kan også ses på som utgangspunktet for en graf. mange av de samme metodene og prinsippene gjelder, bare at vi har rettede og urettede kanter som kanskje har en vekt. Eksempelvis så er INORDER-WALK(x) en simplifisert DFS.

Algoritmene skifter navn når de spesialiseres for en av de mer spesialiserte datastrukturene for eksempel MAX-HEAP og binære søketrær.

TREE-INSERT(), TREE-DELETE() og TREE-MAX/MIN tar logaritmisk tid i gjennomsnitt. Logaritmisk tid er det samme som $O(h)$ hvor $h$ er høyden på treet. Høyden på treet er lik $log(n)$. Hvis dette ikke gir mening, sjekk ut denne miniserien på youtube.

Binære søketrær

Et tre er et binærtre dersom hver node har 0-2 barn. I et binært søketre har hvert element en spesifikk orden. Barnet til venstre vil alltid være mindre enn rotelementet, og barnet til høyre vil være større.

Det er umulig å bygge et binært søketre i verste tilfelle like raskt som en haug. Hvis vi klarte det, så hadde vi brutt grensen for sorteringshastighet! Vi kan redusere sorteringsproblemet til:

Bygg binært søketre
Inorder-tree-walk

Siden trinn 2 bare tar lineær tid, så må trinn 1 overholde sorteringsgrensen!

Søking i et binært søketre i forhold til i en array

Det binære søketreet finner elementet raskere ved at algoritmen kan eliminere elementer som ligger langt unna mål-elementet. Man kan sammenligne denne strategien med binærsøk hvor man halverer antall elementer man vurderer for hver iterasjon.

Denne ordenen gjør traversering/søking svært effektivt, fordi venstre deltre er mindre enn roten og høyre deltre er større en roten. Slik er hele det binære søketreet strukturert som gjør at vi raskt traverserer treet og slipper å forholde oss til noder som ikke er relevant for ønsket output.

Hvordan en sortert array kan bli omgjort til et søketre

Binære hauger (binary heaps)

En haug/heap er et binær heap dersom det er 0-2 barn.

En binær heap kan aldri være et binært søketre. Dette er fordi en binær heap sorterer alle elementene sine slik at forelderen alltid er større/mindre enn barne-noden. I et binært søketre er alltid venstre barne-node mindre, mens høyre barne-node alltid er større. Dermed, siden sorteringsstrukturen er så vidt forskjellig, vil det aldri være mulig at du får et tre som kan være begge samtidig.

Dynamisk programmering

Dynamisk programmering, som splitt og hersk algoritmer, løser problemer ved å kombinere løsninger på delproblemer, ofte rekursivt. Hvis delproblemene overlapper kan man lagre svaret fra et delproblem for å løse problemet i andre. Dynamisk programmering gjelder når delproblemenes delproblem er like. Det er i slike tilfeller splitt og hersk algoritmer gjør mer arbeid enn nødvendig, da de vil løse disse problemene på nytt og på nytt, imens dynamisk programmering sørger for at svar fra like del-delproblemer er lagret i en tabell.

Dynamisk programmering skjer typisk i optimaliseringsproblemer.

Krav til DP:

Optimal delstruktur (løsningen er en kombinasjon av optimale løsninger på delinstansene)
Overlappende delproblemer
Typisk rekursjon, men ikke alltid

Hvordan gjøre det i praksis?

Memoisering (top-down problemløsning)
Iterasjon (bottom-up problemløsning)

Memoisering (top-down)

Memoisering innebærer at man cacher løsninger på delproblemer for så å kunne sette dem sammen for å finne den optimale løsningen på problemet.

F = [-1]*50 # array to store fibonacci terms

def fibonacci_top_down(n):
  if (F[n] < 0):
    if (n==0):
      F[n] = 0
    elif (n == 1):
      F[n] = 1
    else:
      F[n] = fibonacci_top_down(n-1) + fibonacci_top_down(n-2)
  return F[n]

Iterasjon (bottom-up)

F = [0]*50 # array to store fibonacci terms

def fibonacci_bottom_up(n):
  F[n] = 0
  F[1] = 1

  for i in range(2, n+1):
    F[i] = F[i-1] + F[i-2]
  return F[n]

Konstruere løsning fra lagrede beslutninger

Optimal delstruktur og overlappende delinstanser

Optimal delstruktur vil si at løsningen er en kombinasjon av optimale løsninger på delinstansene (delproblemene).

Overlappende delinstanser vil si at løsnmingene på delinstansene lagres og kan gjenbrukes flere ganger til å løse det overordnede problemet, i stedet for at de løses på nytt og på nytt.

Hva om vi ikke har overlappende delproblemer? Da kan vi ikke bruke memoisering da det ikke er noe hensikt i å huske svarene.

Stavkutting og LCS

Stavkutting: Rod cutting
LCS: Longest Common Subsequence - lengste felles subsekvens

Stavkuttingsproblemet

Du har en stav av størrelse $n$ som skal deles i biter og selges for størst fortjeneste. Forskjellige størrelser selges for forskjellige priser.

La $n=7$ og $p=[1,4,3,6,8,5,9]$ være en instans av stavkuttingsproblemet. Hva blir den maksimale inntekten, $r_7$?

$$4+8 = 12$$ $$4+4+4+1 = 13 \Rightarrow r_7$$

Lengste felles subsekvens (LCS)

Vi vil finne hvilke sett med bokstaver som kommer i en sekvens, altså lengste felles subsekvens mellom strengene.

String1: a b c d e f g h i j
String2: e c d g i

e g i er en subsekvens. c d er ikke med da de kommer før e i String1.
c d g i er også en subsekvens, og den lengste. e kan ikke være med da den er i en annen rekkefølge i String1.

String1: s t o n e
String2: l o n g e s t

Vi løser med memoisering til tabell slik LCS-LENGTH ville gjort. Kolonne A/B og Rad 1/2 er henholdvis strengene/indekser. Vi bruker ikke indeks 0 for enkelhets skyld.

Vi starter øverst til venstre (C3) og øker med 1 ved første match s, som følger oss helt til høyre selv om det ikke er flere matcher.

Starter øverst til venstre (altså indeks 1-1) og beveger oss til høyre, og øker ved første match s, som følger oss resten av raden.
Neste kolonne øker når kolonnen over har økt, eller ved match. Neste match her er t på indeks 2-7, som økes med en.
Gjenta punktet over. Neste match er o på indeks 3-2, som følges hele veien til høyre.

		l	o	n	g	e	s	t
	0	1	2	3	4	5	6	7
s	1	0	0	0	0	0	1	1
t	2	0	0	0	0	0	1	2
o	3	0	1	1	1	1	1	2
n	4	0	1	2	2	2	2	2
e	5	0	1	2	2	3	3	3

Ut i fra denne tabellen vet vi at LCS sin lengde er 3, som vist nederst til høyre. Vi leser LCS'en på tabellen ved å se fra venstre til høyre at første gang vi ser 1 er o, 2 er n, og 3 er e.

LCS = o n e.

Ved bruk av memoisering, altså dynamisk programmering, har LCS en kjøretid på O(m*n), hvor m og n er størrelsene på substring M og substring N. Ved en brute-force metode har LCS en eksponensiell kjøretid.

Ryggsekkproblemet (0-1 knapsack)

Ryggsekkproblemet handler om å finne maks verdi man kan ha i en begrenset kapasitet. Det binære ryggsekkproblemet er en variasjon hvor man enten kan legge til en ting eller ikke (til forskjell for det kontinuerlige ryggsekkproblemet, som kan løses grådig). Problemet kan representeres som en binærstreng, hvor 0 er å ikke ta med en ting, og 1 er å ta med en ting.

Benyttes en brute-force metode på det binære ryggsekkproblemet, får løsningen en eksponentiell kjøretid $O(2^n)$. Løses det med dynamisk programmering, får derimot løsningen en kjøretid på $O(n\cdot w)$, hvor $n$ er antall ting å velge blant og $w$ er ryggsekkens vektskapasitet.

Et eksempel på oppgave: Med en ryggsekk som tar vekt $8$, hvilke av de fire tingene bør tas med for å få maks verdi?

$P$ = price = $(1, 2, 5, 6)$.
$W$ = weight = $(2, 3, 4, 5)$.

Ryggsekkproblemet kan løses på lignende måte som LCS-problemet; ved bruk av en tabell. Kolonnene representerer vekt fra 0 til 8. Radene representerer ting. For hver rad tar man kun hensyn til radene over.

Øverste rad er vektkapasiteten til ryggsekken.

			2	3	4	5	6	7	8
$P_i$	$W_i$	# of Item	0	0	0	0	0	0	0
1	2	1	1	1	1	1	1	1	1
2	3	2	1	2	2	3	3	3	3
5	4	3	1	2	5	5	6	7	7
6	5	4	1	2	5	6	6	7	8

Tabellen initieres med 0 verdier i kolonne 0 og rad 0, siden ingen ting er valgt ennå, og har dermed ingen verdi.
I rad 1 vurderes første ting, som har en vekt på 2. Først ved kolonne 2 legges inn tingen, som har en verdi på 1. Ingen flere ting kan velges for denne kolonnen, siden det for denne raden kun er en ting tilgjengelig.
I rad 2 gjentas gjentas kolonnene man fant frem til første verdi, her 1. Ting 2 kan man først legge inn i kolonne 3 (vekt på 3), og legger inn verdi 2. Med rad 2, har man to ting tilgjengelig og kan også velge å putte inn ting 1. Ting 1 har en vekt på 2, og kan legges inn på 5 (3+2).
I rad 3 har man en ting på vekt 4. Vi legger inn dens verdi på kolonne 4, altså verdien 5. Kolonnene før beholder sin verdi. Ting 3 kan kombineres med ting 1, og får en vekt på 6 med verdi 6. Ting 3 kan kombineres med ting 2 og får en vekt på 7 med verdi 7. Ting 3 kan ikke kombineres med ting 1 og 2 da det overstiger kapasiteten på 8. I vekt 5 legges inn 5; det som er maks av det over og til venstre.
I rad 4 har man ting4 på vekt 5, og verdien 6 legges inn. Ting4 kombineres med ting1 til en vekt på 7 med verdi 7. Ting4 kombineres med ting2 til en vekt på 8 med verdi 8.
Nå er alle tingene gjennomgått, og vi ønsker å finne hvilke ting som ble valgt.
Vi starter nederst til høyre, og finner maks på 8. Tallet 8 er ikke funnet i andre rader, så ting4 skal være med i maksfunnet.
Ting4 har verdi på 6. Maksverdi er 8. Det gjenstår å finne ting på verdi 2 (8-6). Første gang verdien 2 vises er i rad 2. Det betyr at ting2 skal være med.

Vi har nå funnet tingene som skal være med i ryggsekken for å gi mest mulig verdi. Løsningen kan representeres som en binærstreng: 0101, hvor ting2 og ting4 tas med.

Grådige algoritmer

Grådige algoritmer er motpælen til dynamisk programmering. I stedet for å velge forskjellige valg underveis, vil en grådig algoritme velge den løsningen som ser mest lovende ut der og da. Grådige algoritmer er ofte enkle å implementere, men det kan være utfordrende å se hvilke problemer de løser optimalt. For å bruke grådige algoritmer må vi ha:

Grådighetsegenskapen: vi må garantert finne en global optimal løsning ved å ta lokalt optimale valg. Det grådige valget må velge et element som en annen optimal algoritme også hadde valgt.
Optimal delstruktur: Optimal løsning bygger på optimale delløsninger, så hvert valg må kun gi ett nytt delproblem. Hvis ikke må vi løse ting på en helt annen måte etter første valg.

Disse egenskapene sammen gir en optimal løsning.

Nøkkeleksempler innen grådig programmering

Aktivitetsutvalg

Man har et sett aktiviteter som starter og slutter på forskjellige tider, og ønsker å gjennomføre flest mulig uten overlapp.

Sorter aktivitetene etter slutt-tid
Velg den første aktiviteten i den sorterte lista (som slutter først)
For hver aktivitet gjenstående i den sorterte lista: om start-tid $\geq$ slutt-tid av forrige aktivitet, legg til aktiviteten. (Grådig valg)

Ryggsekkproblemet

Det binære ryggsekkproblemet - The 0-1 knapsack problem

Huffmankoder og huffmans algoritme

Huffmans grådige algoritme lager prefixer basert på frekvensen av forekomsten av f.eks bokstaver en tekst.

Huffman algoritmen konstruerer optimale prefixkoder basert på grådighetsegenskapen og optimal delstruktur.

Slik ser konstruksjonen av et huffman tre med huffman prefix koder ut. Legg merke til at de bokstavene med lavest forekomst kommer lengst ned og får den lengste bitverdirepresentasjonen. Bokstavene som har hyppigst forekomst i orginalteksten har den korteste veien i treet og forekommer høyere opp. dette gjør akksess av de mest brukte bokstavene raskere.

Huffmankoder er en måte å kode data som består av tegn på en slik måte at den tar minst mulig plass. Selve kodingen defineres av et Huffman-tre som gir informasjonen som trengs for kode en streng med data, for å dekode den igjen. Selve treet konstrueres grådig basert på frekvensen til hvert tegn i inputdataen.

Huffmans algoritme er en grådig algoritme som komprimerer data veldig effektivt, vanligvis mellom 20%-90%. Algoritmen bruker en tabell som teller antall hendelser av hvert tegn i en sekvens med tegn, og bygger et binærtre basert på frekvensene.

Lage trær ut av Huffman frekvenser: "Stryk ut 2 og legg til en"
Eksamensforelesning H19, video 5, 6 min inn

Traversering av grafer

Vi traverserer en graf ved å besøke noder vi vet om. Vi vet i utgangspunktet bare om startnoden, men oppdager naboene til dem vi besøker. Traversering er viktig i seg selv, men danner også ryggraden til flere mer avanserte algoritmer.

Traversering har matching som motivasjon:

Vi husker hvor vi kom fra.
Vi besøker ikke samme node mer enn en gang
- Vi lager et traverseringstre. Finner stier fra startnoden til alle noder vi når fram til.
Vi besøker noder, oppdager noder langst kanter og vedlikeholder en huskeliste.

Grafrepresentasjoner:

En graf er en samling av noder og kanter (edges). Det finnes rettede elller urettede kanter. Kanter kan representeres ved:

Nabomatriser
Nabolister

Man sier ofte at det er raskere med nabomatriser men at de tar mer plass.

Nabomatriser

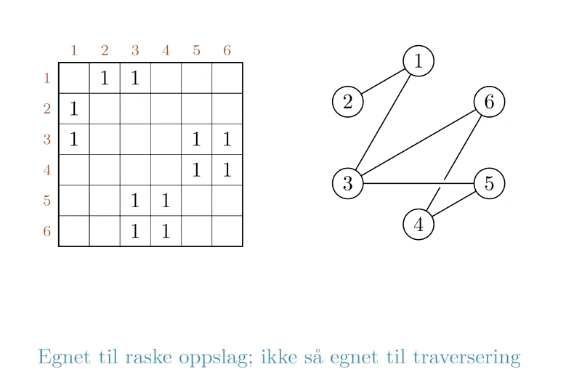
En nabomatrise leses fra rad til kolonne. Det går raskt å slå opp en spesifikk kant, men den er mindre praktisk for traversering.

Viser forholdet mellom noder ved hjelp av en matrise og verdier for eksistens av forhold.

Spørsmål: Er 5 nabo med 4?

Svar: Sjekk rad 5 kolonne 4. Hvis det står "1", ja, da er de naboer med et forhold fra 5 til 4 $(5 \rightarrow 4)$. I figuren er det vist et symmetrisk forhold. Det innebærer at 5 er nabo med 4 og 4 er nabo med 5. Grafen er urettet.

Godt egnet til raske oppslag, ikke så mye til traversering: For oppslag trenger du kun å sjekke rad for så å sjekke respektiv kolonne for å finne ut om et forhold eksisterer. For traversering må man gå over flere ruter som ikke har noe innhold for å sjekke en hel rad. I tillegg kan nabomatriser fort ta mye plass.

De fleste algoritmer bruker $\Omega(V^{2})$ operasjoner med nabomatriser, der $V$ er antallet noder (vertices). Det finnes unntak! (Se kjendisproblemet fra forelesning 8)

Nabolister

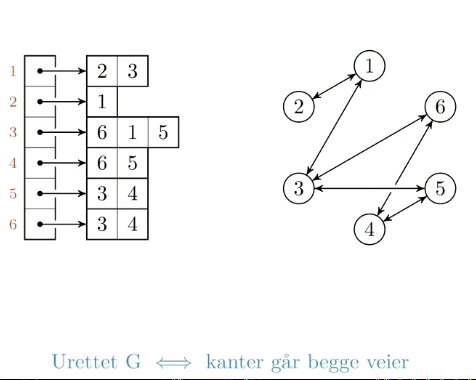
Liste (eller tabell) med ut-naboer for hver node

Spørsmål: Hvem er naboen til 5?

Svar: Sjekk indeks 5, se igjennom listen. Naboene til 5 er 3 og 4.

Godt egnet til traversering, men dårligere til oppslag: For traversering er nabolister en kompakt metode der vi ikke trenger å gå innom noder som ikke har noe forhold. For oppslag må vi derimot gå igjennom lenger lister dersom det er mange pekere på forskjellige noder. Dersom grafen har få kanter vil nabolister også ta mindre plass enn nabomatriser.

Valg av representasjon: Tommelfingerregel

Har du en "sparse" graf, altså at antallet kanter er betydeligere mindre enn max $(m < n^2)$; Er naboliste bedre. (Dersom du hadde valgt nabomatriser hadde du ikke utnyttet hele matrisen og du hadde hatt kolonner og rader som kanskje bare er helt tomme)
Har du en "dense" graf, altså at antallet kanter er $\approx n^2$ så er en nabomatrise gunstig. Den senker kjøretiden fordi den gjør oppslag uten for mye overhead.

Breadth first search (BFS)

En måte å tenke på BFS: Si ifra til naboer at du kommer på besøk i størrelsesorden, besøk i samme rekkefølge som du sa ifra.

Svært effektiv når man har en graf med kanter som er like lange.

Baseres på farging av nodene ved traversering med en FIFO kø. Hvit: Ikke oppdaget. Grå: Oppdaget, men ikke besøkt. Svart: Besøkt og ferdig.

Best case	Worst case
$\Theta(V)$	$\Theta(V+E)$

Hver node & kant blir sjekket en gang.

Depth first search (DFS) og parentesteoremet

Link til DFS

DFS er ca det samme som BFS, men med en LIFO-kø. (Last in first out). BFS traverserer en gang fra startnoden; DFS får ikke inn noen startnode (i vårt emne), den traverserer hver node etter tur.

DFS kan brukes som subrutine, blant annet i Topological sort.

En måte å tenke på DFS: Besøk oppdagede noder umiddelbart.

Parentesteoremet

Noder oppdages før og avsluttes etter sine etterkommere. Hvis de ikke er etterkommere av hverandre, oppdages og avsluttes de før de andre. Finnes dete en sti i mellom dem er det no prob.

DFS og klassifisering av kanter

Kantklassifiseringer:

Møter en hvit node: Tre-kant
Møter en grå node: Bakoverkant (ikke på en DAG)
Møter en svart node: Forover- eller krysskant.

Best case	Worst case
$\Theta(V+E)$	$\Theta(V+E)$

DFS med stakker

Topological sort

Når man har en behov for rekkefølge på nodene i en DAG (directed acyclic graph), kan vi utføre topological sort. Sorteringen legger foreldre før barn, evt sorterer alle slik at de kommer etter sine avhengigheter.

Topologisk sortering gir en ordning av nodene, som respekterer retningen på kantene. Gir nodene en rekkefølge. Samme som gjøres i delproblemgrafen i dynamisk programmering.

En topologisk sortering er ikke nødvendigvis unik. Det kan finnes flere enn en topologisk sortering for en graf.

I DP med memoisering utfører vi implisitt DFS på delproblemene. Vi får automatisk en topologisk sortering fordi problemer løses etter delproblemer. Samme som å sortere etter synkende finish tid.

Kjøretid: $O(V+E)$

Traverseringstrær

Bredde-først-tre

Et bredde-først-tre er et tre som blir lagd under bredde-først-søk. Søket kartlegger hver node i treet som kan nås fra kilde-noden på en uniform måte (bredde før dybde). I denne prosessen regner den ut korteste distanse fra kilden til hver node og lagrer den i et nytt tre. Dette treet er et bredde-først-tre.

Dybde-først-tre

Dybde-først-søk søker så langt ned i grafen som mulig. Den gjør dette ved å velge en vilkårig barne-node som den videre søker nedover i.

Når den treffer bunnen (en løvnode), går den stegvis tilbake til den finner nye barne-node å besøke. Denne prosessen repeteres til alle noder som kan nås fra kilden har blitt utforsket.

Dybde-først-søket produserer ett eller flere trær (en skog) avhengig av hvor mange kilder den trenger for å nå alle nodene. Altså får vi en dybde-først-skog med flere under-dybde-først-trær. Teknikken som blir brukt garanterer at hver node finnes i nøyaktig ett dybde-først-tre i skogen. På den måten får man ikke overlapp mellom under-trærne.

I tillegg til å lage skogen, lagrer også søket tidsstempler på nodene. Disse stemplene lagrer tiden noden ble først oppdaget og tiden når nodens undernoder ble ferdig utforsket. Dette kalles starttid (start-time) og slutttid (finish-time).

Traversering med vilkårlig prioritetskø

Minimale spenntrær

En graf med vekter på kantene. Et minimalt spenntre på en graf er innom alle nodene nøyaktig en gang og har den lavest mulige kombinerte kantvekten. Erke-eksempel på grådighet: Velg én og én kant, alltid den billigste lovlige.

Disjunkte mengder

En disjunkt mengde vedlikeholder en samling $S=[S_1,S_2 ...,S_k]$ av disjunkte dynamiske sett. Vi identifiserer hvert sett med en representant som ikke kan være i andre sett (disjunkt).

MAKE-SET(x) lager et nytt sett hvor $x$ er eneste medlem
UNION(x, y) forener to sett som inneholder $x$ og $y$ til et nytt sett med unionen av de to, og fjerner de fra samlingen
LINK
FIND-SET(x) returnerer peker til settet med $x$.

En av bruksområdene til disjunkt mengde datastrukturen er å kunne definere de koblede komponentene i en urettet graf.

CONNECTED-COMPONENTS(G) bruker operasjonene over til å regne ut de koblede komponentene i grafen
SAME-COMPONENT(u,v) svarer på om to noder er i den samme koblede komponenten

Disjunkte mengder kan representeres som rotfestede trær, der hver node inneholder ett medlem og hvert tre representerer ett sett. I en disjunkt-sett-skog peker hvert element kun til sin forelder, og roten til hvert tre inneholder representativen og sin egen forelder.

Samlet kjøretid for disse operasjonene er $O(m \lg n)$, der $m$ er antall MAKE-SET/UNION/FIND-SET operasjoner og $n$ er antall MAKE-SET operasjoner. Antakelse om at de $n$ MAKE-SET er de første $n$ operasjonene.

Spenntrær og minimale spenntrær

Generisk-MST (Generic-MST):

Vi har en graf:

Delgrafer: Delmengder av nodene. Vi kan ikke ha kanter som ikke er koblet til noder.

Spenngrafer: Delgrafer som spenner over hele den opprinnelige grafen. Den inneholder alle de opprinnelige nodemengdene og en delmengde av den opprinnelige kantmengden.

Spennskoger: Asykliske spenngrafer.

Spenntrær: Sammenhengende spennskoger.

Vi innfører vekter på kantene. Disse kan tolkes som lengder eller kostnader.

Vi vil knytte sammen nodene billigst mulig.
Det kan være flere minimale spenntrær. F.eks. om vi har flere kanter som har samme vekt.

Problemet:

Input: En urettet graf $G = (V,E)$ og en vektfunksjon $w : E \rightarrow \mathbb{R}$.
Output: En asyklisk delmengde $T \subseteq E$ som kobler sammen nodene i $V$ og som minimerer vektsummen: $$w(T)=\sum_{(u,v)\in T}w(u,v)$$

Hvordan løse dette?

Grådig: Vi utvider en asyklisk kantmengde (partiell løsning) gradvis.
Invariant: Kantmengden utgjør en del av et minimalt spenntre.
Hvordan skal vi utvide kantmengden som er en del av et minimalt spenntre, og beholde invarianten?
- Ved å finne en såkalt "trygg kant" som er en kant som bevarer invarianten.

Algoritme for generisk-MST:

GENERIC-MST(G,w)
1    A = Ø
2    while A does not form a spanning tree
3      find an edge (u,v) that is safe for A
4      A = A ⋃ {(u,v)}
5    return A

Hva er trygt å legge til? Hvilken form for grådighet?

Snitt/Cut: Et snitt over en graf. Vi klipper grafen i to. (Figuren under)

Det respekterer kantmengden: Det er ikke klippet noen kanter mellom noder som er svarte og noen som er hvite. Det er ingen kanter som går mellom hvite og svarte noder.
Lett kant: Kanten (4,3) er en (unik) lett kant over snittet (verdi 7): Det er den kanten med lavest vekt av de som er over snittet. (Kantene over snittet på grafen under har verdiene 8, 11, 7, 14 og 10)

Et vekslingsargument: For å vise at det er trygt å velge en lett kant over et snitt som respekterer løsningen vår. Hvis ikke risikerer vi å få en sykel. Vi må kunne dele kantmengdene våre i to separate mengder.

Fremgangsmåte:

Ta en optimal (eller vilkålig) løsning som ikke har valgt grådig. (Som ikke har valgt den lette kanten over det snittet).
Vist at vi kan endre til det grådge valget uten å få en dårligere løsning.

Lette kanter er trygge kanter

I et minimalt spenntre må vi dekke alle nodene på den måten som når minst totalvekt uten sykler.

Lette kanter er trygge fordi vi vet at den kanten med lavest vekt over et snitt i en graf må være med i det minimale spenntreet på grafen. Dermed er det trygt å si at denne kanten er den del av en løsning på problemet som en helhet.

MST-Kruskal

Link til MST-Kruskal

Kruskal sier at en kant med minimal vekt blant de gjenværende er trygg så lenge den ikke danner sykler.

Hvis du utfører MST-Kruskal på grafen under, hvilken kant vil velges som den femte i rekken? Det vil si, hvilken kant vil være den femte som legges til i løsningen? Oppgi kanten på formen $(i, j)$, der $i < j$.

Løsningsforslag

LF = ${(1,4),(2,5),(3,6),(4,5),(5,6)}$, hvor $(5,6)$ er svaret.

MST-Prim

Link til MST-Prim

Korteste vei fra én til alle

Når er det bra å bruke hvilken SP algoritme?

Bredde-først-søk kan finne stier med færrest mulig kanter, men hva om kantene har ulik lengde? Det generelle problemet er uløst, men vi kan løse problemet med gradvis bedre kjøretid for grafer (1) uten negative sykler; (2) uten negative kanter; og (3) uten sykler. Og vi bruker samme prinsipp for alle tre!

Ulike varianter av korteste-vei- eller korteste-sti-problemet

En enkel sti (simple path) er en sti uten sykler. Den korteste veien er alltid enkel.

Single source shortest path (SSSP): en startnode med korteste vei til alle andre
Single destination/target: alle til en. Løses som SSSP i omvendt graf
En til en: samme som SSSP algoritmer da det ikke finnes noe asymptotisk bedre
All pairs shortest path: alle til alle

DAG: Directed Asyclic Graph (rettet asyklisk graf)

Om det finnes en negativ sykel er ingen sti kortest.

Negative sykler gir mening for korteste enkle vei

Korteste enkle vei kan løses vha. lengste enkle vei og omvendt

Representasjon av korteste-vei-tre

Kantslakking

Kantslakking er en oppspalting av minimumsoperasjonen fra dekomponeringen.

$$\delta(s,v) \leq v.d$$

$\delta(s,v)$ er avstanden fra en node $s$ til en node $v$, altså lengden til korteste vei.

$v.d$ er avstandsestimatet vårt, som starter som $\infty$ og blir alltid endret til den beste veien vi har funnet så langt. Denne vil alltid være en faktisk avstand da vi kun reduserer når vi faktisk finner en vei. Idéen er at denne slakkes helt ned til optimum.

Relax

Take it eeeeeeeeeasy. Brukes som subrutine i f.eks. DAG-Shortest-Path og Bellman Ford. Bellman Ford er nesten kun basert på å slakke alle kantene til det "må" bli rett.

  RELAX(u,v,w):
    if v.d > u.d + w(u,v):
      v.d = u.d + w(u,v)
      v.pi = u

Der $v.d$ er avstanden til etterfølgere, $u.d$ er avstanden fra forgjenger og $w(u,v)$ er vekten av kanten mellom forgjengernode v og etterfølgernode u. Forklart: Sjekk om avstand til etterfølgere er større enn summen av avstanden fra forgjenger + vekten av kanten mellom forgjengernode v & etterfølgernode u.

Bellman-Ford

Vi slakker alle kantene helt til det må bli rett

Link til Bellman-Ford

DAG Shortest path

Link til DAG-Shortest-Path

Top-down: Delproblemer er avstander fra startnoden til inn-naboer; Velg den som gir best resultat.

Bottom-up: "Pushing", kantslakking av inn-kanter i topologisk sortert rekkefølge, eller "Pulling", vi drar med oss info fra forgjengerne.

Dijkstras algoritme

Link til Dijkstra

Korteste vei fra alle til alle

Vi kan finne de korteste veiene fra hver node etter tur, men mange av delinstansene vil overlappe – om vi har mange nok kanter lønner det seg å bruke dynamisk programmering med dekomponeringen «Skal vi innom k eller ikke?»

Forgjengerstrukturen for alle-til-alle varianten av korteste vei problemet (Print-All-Pairs-Shortest-Path)

Floyd-Warshall algoritmen

Link til Floyd-Warshall

Transitive-Closure

Vi får en graf eller en binær relasjon. Hvis det finnes en sti fra $u$ til $v$ vil vi legge inn en kant fra $u$ til $v$ slik at vi kan gå direkte.

Link til Transitive-Closure

Johnsons algoritme

Link til Johnsons algoritme

Maksimal flyt

Et stort skritt i retning av generell lineær optimering (såkalt lineær programmering). Her ser vi på to tilsynelatende forskjellige problemer, som viser seg å være duale av hverandre, noe som hjelper oss med å finne en løsning.

Et flytnett er en rettet graf som har en kilde S og en tapp(sluk) T og noder imellom som forbindes med kanter. Hver kant har en kapasitet som viser hvor mye flyt kanten kan motta. Flyt er enheten som blir sendt imellom nodene. Maks-flyt-problemet går ut på å sende mest mulig flyt fra S til T. Det fins algoritmer for å løse dette problemet, blant annet Ford-Fulkerson.

Flytnett: Rettet graf $G=(V,E)$

med kapasiteter $c(u,v) \ge 0$
med en kilde og et tapp(sluk) $s,t \in V$
antakelse: Alle noder er på en sti fra $s \rightarrow t$ $v \in V \Rightarrow s ⇝ v ⇝ t$
ingen self-loops (men vi kan ha sykler bestående av minimum 3 noder)
tillater ikke antiparallelle kanter, det vil si en sykel mellom kunto noder $(u,v)\in E \Rightarrow (v,u) \notin E$
ingen kapasitet uten en kant $(u,v) \notin E \Rightarrow c(u,v) = 0$

Flyt: En funksjon $f : V \times V \rightarrow \mathbb{R}$. Vi kan ha flyt fra enhver node til en annen.

$0 \le f(u,v) \le c(u,v)$
Flyt inn = flyt ut

Flytverdi: $|f| = \sum_vf(s,v)-\sum_vf(v,s)$

Flyt fra kilde til sluk

For å finne flyten i et flytnett kan man summere flyten ut fra kilden.

Maks-flyt-problemet

Hvordan finne maksimal flyt: Summen av bottleneck-verdier.
Hvordan finne bottleneck-verdiene: Minimum av den resterende kapasiteten på en forøkende sti.
Hvordan finne en forøkende sti: Stier med ubrukte kapasiteter fra kilde til sluk.
- For hver forøkende sti man finner: Maksimer kapasiteten ved å legge til den minste rest-verdien på alle ledd i den forøkende stien.

Maksimal flyt brukes også til å løse matching problemet, f.eks organdonasjon med givere og mottakere.

I figuren under ser vi at i Grafen G har vi:

Fra node $1 \rightarrow 2$
- Kapasitet 9
- Flyt 5
- Restkapasitet 4
Fra node $2 \rightarrow 1$
- Restkapasitet 5

Håndtering av antiparallelle kanter og flere kilder og sluk

Flere kilder og sluk: En måte å håndtere flere kilder og sluk er å lage en "master-kilde" og en "master-sluk" og løse oppgaven på samme måte som når det er én kilde og ett sluk.

Antiparallelle kanter: Putt en node i midten av den ene kanten og få heller 3 kanter. Løs oppgaven på samme måte.

Restnettet til et flytnett med en gitt flyt

Et restnett har en fremoverkant ved ledig kapasitet. Hvis vi fyller opp litt av kapasiteten i en kant med flyt kan vi føre noe av den flyten tilbake og oppheve den. Da lager vi en bakoverkant der det allerede går flyt.

Et residualnettverk indikerer hvor mye flyt som er tillatt i hver kant i nettverkgrafen.

Kapasiteten til restnettet: hvor mye vi kan øke flyten fra en node til en annen

Flytoppheving - oppheve (cancel) flyt

Vi kan "sende" flyt baklengs langs kanter der det allerede går flyt.
Vi opphver da flyten, så den kan omdirigeres til et annet sted.
For å unngå opphoping av flyt i forgjengernoden må flyten dirigeres videre. Flyten kan ikke "stoppe opp". Vi kan da gjøre:
- Oppheve flyten videre bakover til enda en forgjengernode
- Sende flyten fremover langs en annen kant til en annen nabonode enn der den opprinnelig kom ifra.

Det er dette bakoverkantene representerer i restnettet. Vi kan følge disse bakoverkantene for å oppheve flyten i flytnettet.

Når man forøker flyten langs den forøkende stien, må det også minskes flyt langs residualkantene med flaskehalsverdien. Residualkantene fungerer ved at de opphever dårlige forøkende stier som ikke leder til maksflyt. Bakoverkantene i restnettet er der kun om det går flyt i flytnettet. Vi kan følge disse kantene for å oppheve flyten i flytnettet.

Restkapasitet

Fremoverkant:
- kan økes med det som gjenstår i $c(u,v)$
Bakoverkant:
- Kan sende tilbake og omdirigere $f(v,u)$
- Å redusere flyten er det samme som å øke den baklengs.

Forøkende sti (augmenting path)

En forøkende sti (eller flytforøkende sti) er en sti av kanter i restnettet med ubrukt kapasitet (mer enn 0) fra kilde $s$ til sluk $t$. Hvis det ikke er noen forøkende stier fra $s$ til $t$, så har flyten nådd maksimum.

Å forøke flyten betyr å oppdatere flytverdiene på kantene langs den forøkende stien. Dette innebærer å øke flyten med flaskehalsverdien (kanten med minst kapasitet).

Altså: En sti der den totale flyten kan økes

Snitt, snitt-kapasitet og minimalt snitt

Et snitt er en deling av grafen og kantene i flyt-nettverket i to mengder, så S og T er i hver sin mengde. Kantenes flyt summeres opp i en snitt-kapasitet. Det minimale snittet er snittet med lavest snitt-kapasitet.

Hvordan regne ut flyten over et snitt:

NB! Husk at dersom man har beregnet forøkende stier må man maksimere disse som nevnt under "Maks-flyt-problemet" før man regner ut flyten over snittet.

Identifiser hvor mye flyt som går gjennom snittet.
Identifiser hvilken flyt som går inn og ut av snittet, altså som går vekk fra kilden og mot kilden.
Summer flyten som går fra kilden og trekk fra flyten som går mot kilden.

Formel for å regne ut flyten over et snitt ${s,v_2},{v_1,v_3,v_4,t}$: $$f({s,v_2},{v_1,v_3,v_4,t}) = f(s,v_1)+f(v_2,v_4)-f(v_1,v_2)-f(v_3,v_2)$$

Maks-flyt/min-snitt teoremet

Teoremet sier at maks-flyt og min-snittet er det samme.

Ford-Fulkerson-Method og Ford-Fulkerson

Link til Ford-Fulkerson

Så lenge vi finner en sti som kan øke flyten kan vi endre flyten.

Ford Fulkerson-metoden finner maks-flyt ved å stadig finne forøkende stier i restnettet og forøker flyten frem til ingen flere forøkende stier blir funnet.

Edmonds-Karp algoritmen

Link til Edmonds-Karp algoritmen

Maks-flyt kan finne en maksimum bipartitt matching

Input: En bipartitt urettet graf $G=(V,E)$
Output: En matching $M \subseteq E$ med flest mulig kanter, dvs. der $|M|$ er maksimal.

En matching er altså en delmengde av alle kanter, der hver node er tilknyttet maks én kant fra delmengden.

Eksempeloppgave

Hva er flyten over dette snittet etter at vi har økt flyten ved å sende maksimal flyt gjennom den forøkende stien $s$, $v_2$, $v_4$, $t$?

Svar: Det er to ting som er viktig å forstå her.

Hvordan flyt mellom noder fungerer
Hva et kutt er

Når man sender flyt fra en node til en annen, må man sende den flyten videre. Man kan ikke ha en slags "overflow" hvor man sender 4 flyt inn i en node, men bare 2 ut igjen. Det som går inn må ut.

Når vi tar et kutt av et flytnett, deler vi nettverket inn i to ikke-overlappende deler, hvor $s$ er i den ene mengden og $t$ er i den andre. Vi ser bare på flyten over kuttet fra $s$ sin mengde til $t$ sin mengde. I dette tilfellet betyr det at vi kun ser på flyten fra $s$ til $v_1$ og $v_2$ til $v_4$.

Det er fristende å tenke; Maksflyt? Ja, da sender jeg maksimal mengde gjennom nettet og ser hvor mye som når frem. Problemet er at dette ikke er lov med mindre all flyten når frem (som nevnt i avsnittet over).

Vi ser på den forøkende stien og ser at maksflyt der er 7. Dette er fordi det allerede sendes 12 gjennom $v_4$ og $t$ (dette er flaskehalsen vår). Vi regner derfor med at det ikke kan sendes mer enn 19 fra $v_2$ til $v_4$. Sender vi mer, vil flyten bli større enn kapasiteten. Det er ikke lov/mulig.

Vi gjør følgende:

Ser at flyten fra $s$ og over snittet til $v_1$ er 14.
Siden det kommer en flyt på 4 fra $v_1$ til $v_2$, kan vi bare øke flyten fra $s$ til $v_2$ med 7 slik at flyten der blir 15.
Vi ser nå at det flyter 14 + 15 = 29.
Vi har nå en totalflyt på 29 som går over snittet.

Det man ser her er at flyten over snittet ikke kan overstige 29 ettersom det da vil overfylles med flyt i $v_2$. Ja, vi kan i teorien sende 21 i flyt til $v_1$, men da må det sendes 11 i flyt til $v_2$

Heltallsteoremet (integrality theorem)

Heltallsteoremet (26.10): For heltallskapasiteter gir Ford-Fulkerson heltallsflyt.

NP-kompletthet

NP er den enorme klassen av ja-nei-problemer der ethvert ja-svar har et bevis som kan sjekkes i polynomisk tid. Alle problemer i NP kan i polynomisk tid reduseres til de såkalt komplette problemene i NP. Dermed kan ikke disse løses i polynomisk tid, med mindre alt i NP kan det. Ingen har klart det så langt...

Det kreves ikke grundig forståelse av de ulike NP-kompletthetsbevisene

Bra intro til hva hele opplegget handler om:
P vs. NP - The Biggest Unsolved Problem in Computer Science

Problem: abstrakt, binær relasjon mellom input og output
Konkret problem: input og output er bitstrenger
Verifikasjonsalgoritme: sjekker (sertifiserer) om en løsning stemmer (true/false) ved å sammenligne sertifikat/vitne og løsning
Sertifikat: En (bit)streng $y$ som brukes som "bevis" for ja-svar
NP (Non-deterministic Polynomial): Ja-svar har vitner (verifikasjon) som kan sjekkes i polynomisk tid
P: Delmengden av NP som kan løses i polynomisk tid
Co-NP: Nei-svar som har vitner som kan sjekkes i polynomisk tid
NP-hard (NPH) er klassen av problemer som har den egenskapen at alle problemer i NP kan reduseres til dem i polynomisk tid.
NPC er snittet av NP og NPH

Dette er litt kaos til å begynne med, men det blir (litt) bedre.

Sammenhengen mellom optimerings- og beslutningsproblemer

Optimeringsproblemer er som regel vanskeligere enn bestemmelsesproblemer.

Optimaliseringsproblem: finne den mest optimale løsningen, eksempelvis Shortest-Path
- NP-kompletthet gjelder ikke for optimaliseringsproblemer direkte
- Ikke nødvendigvis noe vitne
Beslutningsproblem: ja/nei problemer (1/0)
- Finnes det et vitne?

Selv om NP-komplette problemer hovedsakelig gjelder beslutningsproblemer, er det et praktisk forhold mellom optimalisering- og beslutningsproblemer hvor de kan reformuleres som beslutningsproblemer. Shortest-Path er vanligvis et optimaliseringsproblem, men reformulert kan vi spørre om det finnes en sti under et gitt antall kanter. Her kan algoritmen svare $1$ dersom det finnes, eller $0$ om det ikke finnes, altså et beslutningsproblem. Ved å svare på beslutningsproblemet om det finnes en sti under et gitt antall kanter gjentatte ganger kan vi til slutt finne den korteste stien.

Hvis vi kan bevise at et beslutningsproblem er vanskelig, gir vi også bevis for at det relaterte optimaliseringsproblemet er vanskelig.

Koding (encoding) av en instans av et problem

Om en datamaskin skal forstå et problem, må vi representere det binært, altså konkretisere problemet ved å kode det (encode) til en bitstreng.

Enkoding brukes for å mappe abstrakte problemer som konkrete problemer.
Et abstrakt beslutningsproblem kan mappes som et av instanser, som et relatert konkret beslutningsproblem.
Polynomisk relaterte instanser: Hvis to enkodinger $e1$ og $e2$...

Binære ryggsekkproblemet er ikke polynomisk

Ryggsekkproblemet: Fyll sekken med mest verdi uten å gå over vektgrensen. Ryggsekkproblemet kan løses med dynamisk programmering på en kjøretid på $O(n\cdot w)$, så hvorfor omtales ikke det binære ryggsekkproblemet som polynomisk?

Svaret handler om forholdet mellom binærrepresentasjon av input og hvor lang tid programmet faktisk tar å kjøre. Lurt å se video om dette: Why is the knapsack problem pseudo-polynomial?

Et eksempel som kan vise dette forholdet er en enkel for-løkke:
En for-løkke går fra $1 \rightarrow n$. Datamaskinen forstår binærtall, så $n$ må gjøres om fra tall til binærtall. 4 til 100, 8 til 1000, 16 til 10000. For hver økning av binærtall, dobles det faktiske tallet.

Så over til det binære ryggsekkproblemet.

Kjøretiden til ryggsekkproblemet omtales fortsatt som $O(nw)$, selv om det er ubundet, hvor $n$ representerer ting og $w$ representerer kapasitet. $n$ kan representeres som en liste, som stadig får flere ting i seg ettersom input øker. $w$ derimot representeres som et tall, og ettersom $w$ blir større, blir den flere bits lengre:

F.eks. om $W = 1.000.000.000.000$, representeres dette med 40 bits. Inputstørrelsen er 40, men kjøretiden vil være $O(2^{40})$. Dermed blir kjøretiden eksponensiell.

Kjøretiden omtales som pseudopolynomisk siden den ser polynomisk ut $O(nw)$, men ikke i virkeligheten er det $O(n \cdot 2^{bits \ i \ w})$.

Forskjellen på konkrete og abstrakte problemer

Kort: Et konkret problem er representert som en streng av bits som kan løses av en datamaskin. Et abstrakt problem er mer "ideen" av problemet, en binær relasjon mellom input og output.

Representasjon av beslutningsproblemer

Konkrete beslutningsproblemer tilsvarer formelle språk (mengder av strenger). Ja-instanser er med, nei-instanser er ikke.

Det "motsatte" er abstrakte beslutningsproblemer, som en datamaskin ikke kan løse direkte.

Definisjon av klassene P, NP og co-NP

Kompleksitetsklasse: en måte å klassifisere problemer basert på tiden som kreves for å finne en løsning. For å forenkle klassifiseringen omformuleres alle oppgaver slik at de kan avgjøres med ja eller nei.

Kompleksitetsklasser av problemer:

P: kan løses i polynomisk tid
- Språkene som kan avgjøres i polynomisk tid
NP: kan løses ikke-deterministisk i polynomisk tid,
- Språkene som kan verifiseres i polynomisk tid
- HAM-Cycle $\in$ NP: språket for hamilton-sykel-problemet.
Co-NP: Språkene som kan falsifiseres i polynomisk tid
- $L \in$ co-NP $\leftrightarrow \bar{L} \in$ NP

Oppsummert, så er da:

P problemer raske å løse
NP problemer raske å verifisere men trege å løse
NP-komplette problemer er også raske å verifisere og trege å løse, men kan bli redusert til hvilket som helst annet NP-komplett problem
NP-harde problemer er trege å verifisere, trege å løse, og kan bli redusert til hvilket som helst annet NP-problem

P vs NP

Vi forholder oss til venstre side av diagrammet. Reduksjon skjer "oppover" i diagrammet.

Resubilitetsrelasjonen $\leq_P$

Se reduksjon.

NP-hardhet og NP-kompletthet

NP-harde problemer er minst like vanskelige som alle NP-problemer, men ikke nødvendigvis en del av NP. Er de en del av NP, omtales de som NPC.

NP-hardhet: Et problem $Q$ er NP-hardt dersom alle problemer i NP kan reduseres til det.

Et problem er altså NP-komplett dersom det i) er NP-hardt, og ii) er i NP.

Den konvensjonelle hypotesen

P kan reduseres til alt $\rightarrow$ alt kan reduseres til NPC.

Kompletthet:

Et problem er komplett for en gitt klasse og en gitt type reduksjoner dersom det er maksimalt for redusibilitetsrelasjonen.
- De komplette problemene er de vannskeligste i klassen.
Et element er maksimalt dersom alle andre er mindre eller lik. For alle reduksjoner: Q er maksimalt dersom alle problemer i klassen kan reduseres til Q.

NPC: De komplette språkene i NP, under polynomiske reduksjoner.

Reduksjon

Definisjon redusibilitet: Hvis $A$ kan reduseres til $B$ i polynomisk tid, skriver vi $A \leq_P B$.

Problemer $A$ og $B$. $A$ er lettere enn $B$. Reduksjon er å vise at $A \leq_P B$.

Om man skal vise at et problem $X$ er vanskelig, redusér fra et vanskelig problem $Y$, dvs. etablér at $X \leq_P Y$.

Eksempel 1:
Anta at $B$ inneholder nøkkelen til $A$.
Kan det nå være vanskeligere å åpne $A$ enn $B$?
Nei! Om vi kan åpne $B$, så kan vi naturligvis åpne $A$.
Vi har redusert problemet "åpne $A$" til problemet "åpne $B$".
Da gir det ingen mening å si at $A$ er vanskeligere enn $B$.
$A \leq B$
Eksempel 2:
Problem $A$ er i P og problem $B$ er i NP.
For å vise at P = NP, hva må vi redusere fra og til?
$B_{NP}$ -> $A_{P}$.
Eksempel 3:
Problem $A$ er bevist NP og problem $B$ er bevist NP-hardt.
Hvis man finner en polynomisk reduksjon fra $B$ til $A$ har man vist at $A$ er NP-komplett.
B er NP-komplett hvis vi kan verifisere $B$ polynomisk.

Krokodillemunnen spiser samme vei som pilen
Altså vi må redusere $A \leq$ $\rightarrow B$

Alt i NP kan reduseres til NP hardt. Reduksjoner skjer til lik eller høyere kompleksitetsklasser.

Typiske reduksjoner for å bevise NP-kompletthet

Eksempel på NP-komplette problemer

CIRCUIT-SAT: Circuit satisfiability
- En krets med logiske porter og én utverdi
- Kan utverdien bli $1$?
SAT: Satisfiability
- En logisk formel (typ diskmat: $\wedge \vee \neg \to \iff$)
- Kan formelen være sann?
- Kan reduseres til det binære ryggsekkproblemet, hvor i likhet med formelen som tar sannhetsverdier, så kan også om en ting skal legges i ryggsekken representeres som 1 og det å ikke legge til representeres som 0.
3-CNF-SAT
- En logisk formel på 3-CNF-form
- Kan formelen være sann?
CLIQUE: "Sosialt nettverk"
- En urettet graf $G$ og et heltall $k$
- Har $G$ en komplett delgraf med $k$ noder?
VERTEX-COVER
- En urettet graf $G$ og et heltall $k$
- Har $G$ et nodedekke med $k$ noder? Dvs: $k$ noder som tilsammen ligger inntil alle kantene
- Et nodedekke for en graf $G$ har noder som forbinder alle kantene i $G$.
HAM-CYCLE
- En urettet graf $G$
- Finnes det en sykel som inneholder alle nodene nøyaktig en gang?
TSP: Traveling Salesman Problem. Totalt korteste reise som er innom hver by
- Beslutningsproblemet er NP-komplett
- Optimeringsversjonen er NP-hardt
- En komplett graf med heltallsvekter og et heltall $k$
- Finnes det en rundtur med kostnad $\leq k$?
SUBSET-SUM: Delmengde som summerer til en målverdi
- Mengde positive heltall $S$ og positivt heltall $t$
- Finnes en delmengde $S' \subseteq S$ så $\sum_{s\in S'} s = t$?

Det binære ryggsekkproblemet er NP-hardt

Lengste enkle-vei-problemet er NP-hardt

Lengste-vei kan reduseres fra HAM-PATH Hamilton Path problemet: en enkel sti/path som besøker hver node nøyaktig en gang. HAM-PATH er NP-hardt.

Selv om Shortest-Path blir løst i polynomisk tid, så er lengste vei et NP-problem, da her ønsker vi å besøke alle nodene en gang, imens korteste vei krever ikke at vi besøker alle nodene.

Konstruere enkle NP-kompletthetsbevis

Vis at $L \in NP$
Velg et kjent NP-komplett språk $L'$ eller et problem
Beskriv en reduksjon/algoritme som beregner en funksjon $$f : \lbrace 0,1 \rbrace \ast \rightarrow \lbrace 0,1 \rbrace \ast$$ som mapper instanser av $L'$ til instanser av $L$.
Vis at $x \in L' \longleftrightarrow f(x) \in L$, for alle $x \in \lbrace 0,1 \rbrace \ast$.
Vis at algoritmen som beregner $f$ har polynomisk kjøretid.

Kjøretider fra pensum

Sorteringsalgoritmer

Søking

Algoritme	Best case	Average case	Worst case	Minne
Brute force	$O(n)$	$O(n)$	$O(n)$	$O(n)$
Binary search	$O(1)$	$O(\log n)$	$O(\log n)$	N/A

Sammenligningsbaserte sorteringsalgoritmer

Algoritme	Best case	Average case	Worst case	Minne
Merge sort	$O(n \log n)$	$O(n \log n)$	$O(n \log n)$	$O(n)$
Quick sort	$O(n\log n)$	$O(n\log n)*$	$O(n^2)$	$O(\lg n)$
Bubble sort	$O(n)$	$O(n^2)$	$O(n^2)$	N/A
Insertion sort	$\Theta(n)$	$\Theta(n^2)$	$O(n^2)$	$O(1)$
Selection sort	$O(n^2)$	$O(n^2)$	$O(n^2)$	$O(1)$

* randomized-quicksort

Ikke-sammenligningsbaserte sorteringsalgoritmer

Algoritme	Best case	Average case	Worst case	Minne
Heap sort	$O(n)$	???	$O(n \log n)$	$O(1)$
Counting sort	$\Omega(n+k)$	$\Theta(n+k)$	$O(n+k)$	$O(n+k)$
Radix sort	$\Theta(d(n+k))$	$\Theta(d(n+k))$	$\Theta(d(n+k))$	$O(n+k)$
Bucket sort	$\Theta(n)$	$\Theta(n)$	$\Theta(n^2)$	$O(n)$
Topological sort	$\Theta(V+E)$	N/A	$\Theta(V+E)$	N/A

Grafalgoritmer

Traversering

Algoritme	Best case	Average case	Worst case	Minne
Breadth first search	$\Theta(V)$	N/A	$\Theta(V+E)$	N/A
Depth first search	$\Theta(V+E)$	N/A	$\Theta(V+E)$	N/A

Minimal spanning tree

Algoritme	Datastruktur	Tidskompleksitet
Prim	Binary Min-Heap	$O(E\lg V)$
Prim	Fibonacci Heaps	$O(E+V\lg V)$ (bedre)
Kruskal	Disjoint-set skog	$O(E\lg V)$

Korteste vei

En-til-alle (single source shortest path)

Algoritme	Datastruktur	Tidskompleksitet
Dijkstra	Fibonacci heap	$O(V\lg V + E)$
Dijkstra	Binary min-heap	$O(E\lg V + V\lg V)$
Dijkstra	Array	$O(V^2)$
Bellman-Ford	N/A	$O(V\cdot E)$

Alle-til-alle (all pairs shortest path)

Algoritme	Best case	Average case	Worst case
Johnson's algoritme	$O(V^2 \log V + VE)$	$O(V^2 \log V + VE)$	$O(V^2 \log V + VE)$
Floyd-Warshall	$\Theta(V+E)$	N/A	$\Theta(V+E)$

Maks flyt / minimal cut

Gitt en graf $G=(V,E)$ med flyt $f$, ved hver iterasjon finner vi en forøkende sti $p$, og vi bruker $p$ for å endre på $f$.

Algoritme	Info	Best case	Worst case
Ford-Fulkerson	TODO	$O(V\cdot E^2)$	$O(E_f)$
Edmonds-Karp	Ford-Fulkerson med BFS	$O(V\cdot E^2)$	$O(V\cdot E^2)$

Definisjoner

In-place

En in-place algoritme vil ikke allokere mer minne under kjøring for å manipulere input. Det gjelder derimot ikke for det ekstra minnet som blir allokert for variabler.

Overhead

Generelt hvor mye minne som kreves for å utføre en operasjon. I dette emnet kvantifiseres det kun i form av at en algoritme har "mer" eller "mindre" overhead.

Korrekthet

Å sjekke at løkkeinvarianten er riktig før løkka starter, etter hver iterasjon og når løkka er ferdig. Algoritmen gir korrekt output som følge av input.

Pseudopolynomisk

Algoritmer med kjøretider som er polynomiske hvis vi lar et tall fra input være med som parameter til kjøretiden (slik som $\Theta(n*W)$, der W er et tall fra input, og ikke direkte en del av problemstørrelsen) kaller vi pseudopolynomiske.

Problemløsningsguide

Dette er en oppsummering av problemløsningsguiden 2020.

De tre fasene for en god problemløsningsstrategi er:

Tolkning
Analyse
Syntese

I følgende avsnitt blir disse punktene forklart.

Tolkning

Definer problemet eller problemene du står overfor. Klargjør hva din oppgave er: Hva skal du gjøre med problemene?

Analyse

Plukk problemet fra hverandre og plasser det i en større kontekst. List opp alt du har av relevant kunnskap og relevante verktøy.

Syntese

Koble sammen bitene og fyll inn det som mangler av transformasjoner, mindre beregningstrinn og eventuelle korrekthetsbevis.

Distribuert kognisjon

Benytt deg av såkalt distribuert kognisjon, og skriv ting ned. Tegn figurer og diagrammer. Lag lister med alle alternativer du kan komme på. Står du fast, bruk penn og papir, whiteboard eller din favoritt-editor for å prøve å komme videre.

Forbedre løsningen trinnvis

Prøv å komme på eksempler som gjør at du får galt svar. Prøv så å forbedreløsningen, så den håndterer disse eksemplene.

Tenk logisk

Er det noen ting på listene dine som umulig kan være relevante? Er det noe du vet må være sant, som begrenser løsningen? Gir ting mening fra et fugleperspektiv?

Name		Name	Last commit message	Last commit date
Latest commit History 135 Commits
.github/workflows		.github/workflows
.vscode		.vscode
Algoritmer		Algoritmer
Figurer		Figurer
Python		Python
Ressurser		Ressurser
.gitignore		.gitignore
.mdl_style.rb		.mdl_style.rb
.mdlrc		.mdlrc
README.md		README.md
contributing.md		contributing.md

Xtrah/TDT4120

Folders and files

Latest commit

History

Repository files navigation