P-Center Problem (PCP) solver

Solving P1 and P3 formulations from the paper: Calik H, Tansel BC (2013) Double bound method for solving the p-center location problem. Comput Oper Res 40:2991–2999

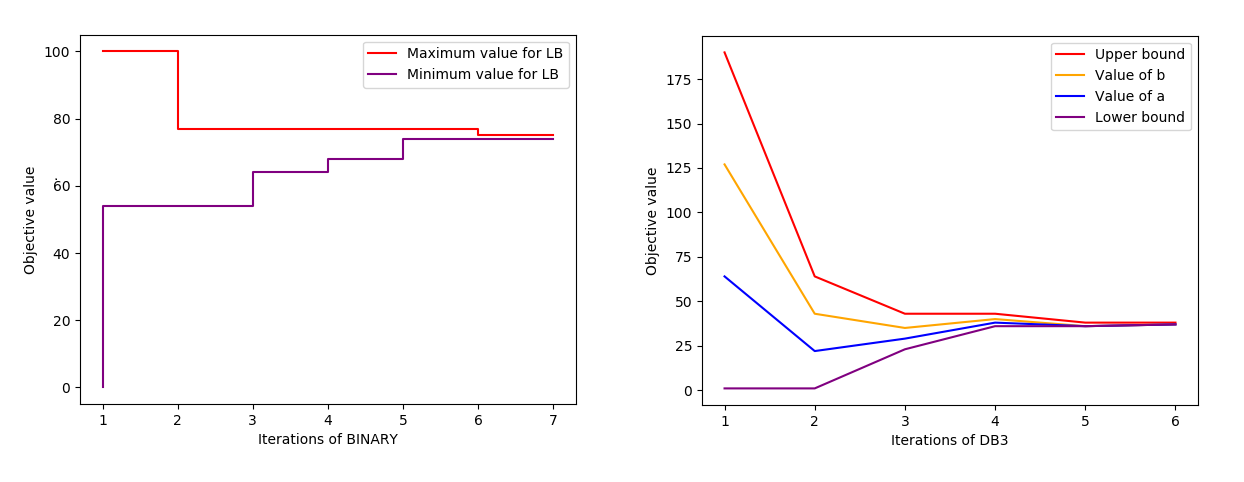
The BINARY and DB3 algorithms from the same paper have been implemented in order to solve P3 efficiently.

Finding bounds for the P3 formulation

Lower bound with BINARY

Lower and upper bounds with DB3

Dependencies

julia> Pkg.add("ArgParse")
julia> Pkg.add("Cbc")
julia> Pkg.add("GLPKMathProgInterface")
julia> Pkg.add("JuMP")

How to run solve.jl

General command syntax:

$ julia solve.jl <path-to-instance> <form> [--solver SOLVER]

Argument "form" must be either "p1", "p3", "p3-binary" or "p3-db3". Argument "solver" can be either "cbc" or "glpk" (default value is "cbc").

The script will create a folder "results" in current directory and write the results for given formulation, instance and solver in a txt file.

Run formulation P1 the fastest way

$ julia solve.jl path-to-instance p1

Run formulation P3 the fastest way

$ julia solve.jl path-to-instance p3-db3