Original research
While most of cpp-sort's algorithms are actually taken from other open-source projects, and/or naive implementations of well-known sorting algorithms, it also contains a bit of original research. Most of the things described here are far from being ground-breaking discoveries, but even slight improvements to known algorithms deserve to at least be documented so that they can be reused, so... here we go.
The vergesort is a new sorting algorithm which combines merge operations on almost sorted data, and falls back to a pattern-defeating quicksort when the data is not sorted enough. Just like TimSort, it achieves linear time on some patterns, generally for almost sorted data, and should never be worse than O(n log n) in the worst case. This last statement has not been proven, but the many benchmarks show that it is only slightly slower than a pattern-defeating quicksort for shuffled data, which is its worst case, so...
Best Average Worst Memory Stable
n n log n n log n n No
While vergesort has been designed to work with random-access iterators, there also exists a version that works with bidirectional iterators. The algorithm is slightly different and a bit slower. Basically, it falls back on a regular quicksort instead of a pattern-defeating quicksort since the latter has to fall back to a heapsort, which only works with random-access iterators. The complexity for the bidirectional iterators version is as follows:
Best Average Worst Memory Stable
n n log n n² n No
This sorting algorithm has been split as a separate project. You can read more about in the dedicated repository.
The double insertion sort is a somewhat novel sorting algorithm to which I gave what is probably the worst name ever, but another name couldn't describe better what the algorithm does (honestly, I would be surprised if it hadn't been discovered before, but I couldn't find any information about it anywhere). The algorithm is rather simple: it sorts everything but the first and last elements of a collection, switches the first and last elements if they are not ordered, then it inserts the first element into the sorted sequence from the front and inserts the last element from the back.
As the regular insertion sort, it comes into two flavours: the version that uses a liner search to insert the elements and the one that uses a binary search instead. While the binary search version offers no advatange compared to a regular binary insertion sort, the linear version has one adavantage compared to the basic linear insertion sort: even in the worst case, it shouldn't take more than n comparisons to insert both values into the sorted sequence, where n is the size of the collection to sort, making less comparisons and less moves than a regular linear insertion sort on average.
Best Average Worst Memory Stable Iterators
n n² n² 1 No Bidirectional
This algorithm was originally used in cpp-sort to generate small array sorts, but it has since been mostly dropped in favour of better alternatives depending on the aim of the small array sort.
A half-cleaner network is a comparison network of depth 1 in which input line i is compared with line i + n/2 for i = 1, 2, ..., n/2. For the sake of simplicity, we only consier networks whose size is even. This kind f network is mostly mentioned to describe a particular step in bitonic sorting networks. I played a bit with half-cleaners to try to create new merging networks. The results are of course not as good as the existing sorting networks, but interesting nonetheless.
When given two sorted inputs of size n/2, a half-cleaner seems to have the following property: the first element of the output will be the smallest of the network and the last element of the output will be the greatest f the network. Moreover, both halves of the output are sorted. That means that it is possible to create what I would call a shrinking merge network that half-cleans the input of size n, then half-cleans the output of size n-2, then half-cleans the output of size n-4, etc... While easy to implement, it is a merging network slower than the most well-known ones and is of depth n/2, which is rather bad...
Anyway, the nice property of this half-cleaning is that it can be performed on networks of any size. It means that it is for example possible to half-clean an input of size 12 (elements 1 and 12 will be in their final position, elements [2-6] and [7-11] are sorted), then to sort the elements 2 and 11 and to perform an odd-even merge on the elements [3-10]. Once again, it does not produce better results than an odd-even merge, but it's easy to implement for any size of arrays and is sometimes as good as an odd-even merge.
While trying to reimplement size-optimal sorting networks as described by Finding Better Sorting Networks, I ended up implementing a sorting network of size 24 whose size was equivalent to that of the one described in the paper (123 compare-exchange units). However, it seems that this sorting network does not use an odd-even merge network but another merge network, obtained by the method described in the previous section. From this network, it was also trivial to generate the corresponding network of size 23, whose size also corresponds to the best-known one (118). Here are the two networks and the corresponding sequences of indices:
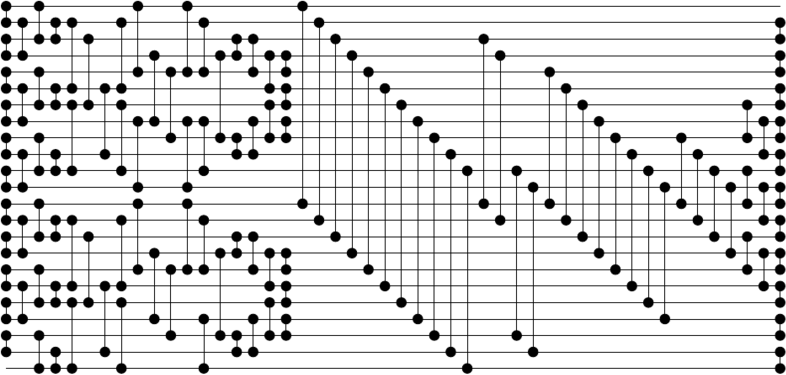
[[0, 1],[2, 3],[4, 5],[6, 7],[8, 9],[10, 11],[12, 13],[14, 15],[16, 17],[18, 19],[20, 21]]
[[1, 3],[5, 7],[9, 11],[0, 2],[4, 6],[8, 10],[13, 15],[17, 19],[12, 14],[16, 18],[20, 22]]
[[1, 2],[5, 6],[9, 10],[13, 14],[17, 18],[21, 22]]
[[1, 5],[6, 10],[13, 17],[18, 22]]
[[5, 9],[2, 6],[17, 21],[14, 18]]
[[1, 5],[6, 10],[0, 4],[7, 11],[13, 17],[18, 22],[12, 16]]
[[3, 7],[4, 8],[15, 19],[16, 20]]
[[0, 4],[7, 11],[12, 16]]
[[1, 4],[7, 10],[3, 8],[13, 16],[19, 22],[15, 20]]
[[2, 3],[8, 9],[14, 15],[20, 21]]
[[2, 4],[7, 9],[3, 5],[6, 8],[14, 16],[19, 21],[15, 17],[18, 20]]
[[3, 4],[5, 6],[7, 8],[15, 16],[17, 18],[19, 20]]
[[0, 12],[1, 13],[2, 14],[3, 15],[4, 16],[5, 17],[6, 18],[7, 19],[8, 20],[9, 21],[10, 22]]
[[2, 12],[3, 13],[10, 20],[11, 21]]
[[4, 12],[5, 13],[6, 14],[7, 15],[8, 16],[9, 17],[10, 18],[11, 19]]
[[8, 12],[9, 13],[10, 14],[11, 15]]
[[6, 8],[10, 12],[14, 16],[7, 9],[11, 13],[15, 17]]
[[1, 2],[3, 4],[5, 6],[7, 8],[9, 10],[11, 12],[13, 14],[15, 16],[17, 18],[19, 20],[21, 22]]
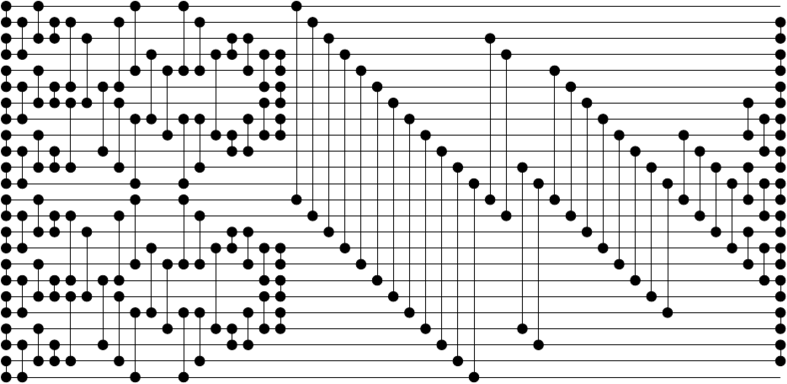
[[0, 1],[2, 3],[4, 5],[6, 7],[8, 9],[10, 11],[12, 13],[14, 15],[16, 17],[18, 19],[20, 21],[22, 23]]
[[1, 3],[5, 7],[9, 11],[0, 2],[4, 6],[8, 10],[13, 15],[17, 19],[21, 23],[12, 14],[16, 18],[20, 22]]
[[1, 2],[5, 6],[9, 10],[13, 14],[17, 18],[21, 22]]
[[1, 5],[6, 10],[13, 17],[18, 22]]
[[5, 9],[2, 6],[17, 21],[14, 18]]
[[1, 5],[6, 10],[0, 4],[7, 11],[13, 17],[18, 22],[12, 16],[19, 23]]
[[3, 7],[4, 8],[15, 19],[16, 20]]
[[0, 4],[7, 11],[12, 16],[19, 23]]
[[1, 4],[7, 10],[3, 8],[13, 16],[19, 22],[15, 20]]
[[2, 3],[8, 9],[14, 15],[20, 21]]
[[2, 4],[7, 9],[3, 5],[6, 8],[14, 16],[19, 21],[15, 17],[18, 20]]
[[3, 4],[5, 6],[7, 8],[15, 16],[17, 18],[19, 20]]
[[0, 12],[1, 13],[2, 14],[3, 15],[4, 16],[5, 17],[6, 18],[7, 19],[8, 20],[9, 21],[10, 22],[11, 23]]
[[2, 12],[3, 13],[10, 20],[11, 21]]
[[4, 12],[5, 13],[6, 14],[7, 15],[8, 16],[9, 17],[10, 18],[11, 19]]
[[8, 12],[9, 13],[10, 14],[11, 15]]
[[6, 8],[10, 12],[14, 16],[7, 9],[11, 13],[15, 17]]
[[1, 2],[3, 4],[5, 6],[7, 8],[9, 10],[11, 12],[13, 14],[15, 16],[17, 18],[19, 20],[21, 22]]