n-queens

N-Queens Problem

The eight queens puzzle is the problem of placing eight chess queens on an 8×8 chessboard so that no two queens threaten each other. Thus, a solution requires that no two queens share the same row, column, or diagonal. The eight queens puzzle is an example of the more general n queens problem of placing n non-attacking queens on an n×n chessboard, for which solutions exist for all natural numbers n with the exception of n=2 and n=3.

For example, following is a solution for 4 Queen problem.

The expected output is a binary matrix which has 1s for the blocks where queens are placed. For example following is the output matrix for above 4 queen solution.

{ 0,  1,  0,  0}
{ 0,  0,  0,  1}
{ 1,  0,  0,  0}
{ 0,  0,  1,  0}

Naive Algorithm

Generate all possible configurations of queens on board and print a configuration that satisfies the given constraints.

while there are untried configurations
{
   generate the next configuration
   if queens don't attack in this configuration then
   {
      print this configuration;
   }
}

Backtracking Algorithm

The idea is to place queens one by one in different columns, starting from the leftmost column. When we place a queen in a column, we check for clashes with already placed queens. In the current column, if we find a row for which there is no clash, we mark this row and column as part of the solution. If we do not find such a row due to clashes then we backtrack and return false.

1) Start in the leftmost column
2) If all queens are placed
    return true
3) Try all rows in the current column.  Do following for every tried row.
    a) If the queen can be placed safely in this row then mark this [row, 
        column] as part of the solution and recursively check if placing  
        queen here leads to a solution.
    b) If placing queen in [row, column] leads to a solution then return 
        true.
    c) If placing queen doesn't lead to a solution then umark this [row, 
        column] (Backtrack) and go to step (a) to try other rows.
3) If all rows have been tried and nothing worked, return false to trigger 
    backtracking.

Bitwise Solution

Bitwise algorithm basically approaches the problem like this:

• Queens can attack diagonally, vertically, or horizontally. As a result, there can only be one queen in each row, one in each column, and at most one on each diagonal.
• Since we know there can only one queen per row, we will start at the first row, place a queen, then move to the second row, place a second queen, and so on until either a) we reach a valid solution or b) we reach a dead end (ie. we can't place a queen such that it is "safe" from the other queens).
• Since we are only placing one queen per row, we don't need to worry about horizontal attacks, since no queen will ever be on the same row as another queen.
• That means we only need to check three things before placing a queen on a certain square: 1) The square's column doesn't have any other queens on it, 2) the square's left diagonal doesn't have any other queens on it, and 3) the square's right diagonal doesn't have any other queens on it.
• If we ever reach a point where there is nowhere safe to place a queen, we can give up on our current attempt and immediately test out the next possibility.

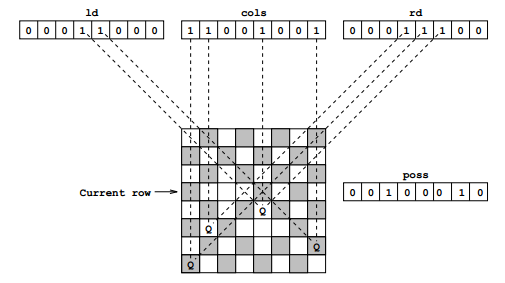
First let's talk about the recursive function. You'll notice that it accepts 3 parameters: leftDiagonal, column, and rightDiagonal. Each of these is technically an integer, but the algorithm takes advantage of the fact that an integer is represented by a sequence of bits. So, think of each of these parameters as a sequence of N bits.

Each bit in each of the parameters represents whether the corresponding location on the current row is "available".

For example:

• For N=4, column having a value of 0010 would mean that the 3rd column is already occupied by a queen.
• For N=8, ld having a value of 00011000 at row 5 would mean that the top-left-to-bottom-right diagonals that pass through columns 4 and 5 of that row are already occupied by queens.

Below is a visual aid for leftDiagonal, column, and rightDiagonal.

References

• Wikipedia
• GeeksForGeeks
• On YouTube by Abdul Bari
• On YouTube by Tushar Roy
• Bitwise Solution
  • Wikipedia
  • Solution by Greg Trowbridge