You signed in with another tab or window. Reload to refresh your session.You signed out in another tab or window. Reload to refresh your session.You switched accounts on another tab or window. Reload to refresh your session.Dismiss alert
Your examples 1,2 look correct. I like how you defined F as a set with the implied pattern in Example 2. Another way to do it would be to describe it as "F(n) is the largest even number less than or equal to n", or as a piecewise "F(n) = n if n is even, and n-1 if n is odd." Once you are comfortable with the idea that a function can be written as a set of pairs, you are certainly not obligated to always write it that way.
You're right that it's hard to prove that your third example is not countable. The problem of determining if a set is not countable is famous problem described in Exercise 4.8, in which I ask you to find a source on the internet that explains it. A while back I wrote a blog post on this topic, in case you're interested to read further.
If the function is bijective, then you for one know that the set is not finite. Generally you say that the set has "cardinality equal to $\mathbb{N}$", and this specific number is given a name: https://en.wikipedia.org/wiki/Aleph_number
Thank you Jeremy for validating my answer - and also providing the feedback, it's very helpful :)
That blog post is intriguing - I need to spend some time to understand it. I cam across some answers on math.stackexchange.com and they mentioned diagnolization but I had no clue about it - now I know something about it :)
All of these answers, pointers, and feedback is really great - much appreciated. Thank you once again.
I just want to ensure if my reasoning w.r.t. the examples I thought of for countable sets is correct or not.
Example 1:
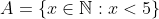
In this case we can write a surjection F: N -> A as follows:

Example 2:
A = {set of all positive even integers}In this case we could write a surjection such as:
F = {(0, 0), (1, 0), (2, 2), (3, 2), (4, 4), (5, 4),...}On the other hand if we define A as

Then it is not possible to define a surjection
F: N -> A(although I am not sure how to prove this).Therefore
Ais not countable.I am wondering what is the implication if the function
F: N -> Ais bijective. Does that have any special meaning?The text was updated successfully, but these errors were encountered: