You signed in with another tab or window. Reload to refresh your session.You signed out in another tab or window. Reload to refresh your session.You switched accounts on another tab or window. Reload to refresh your session.Dismiss alert
The definition of is not clear from the question. I could think of two possible interpretations: is a set consisting of any n natural numbers, or another interpretation is that consists of numbers from 1 to n.
In the latter interpretation, it is pretty straightforward to prove that the union of all such will essentially be N
which has an injective mapping from
In the former case I am confused if it can be shown that there will be a injection from to the union because I can always select arbitrary which always excludes certain numbers from (say none of the has 1) then the union will essentially be . In this case it is easy to show a surjection from to but will it also be an injection because of the their infinite cardinality?
The text was updated successfully, but these errors were encountered:
Suppose for each natural number n we chose a different, countably infinite set $A_n$. I.e., each $A_n$ has a bijection with the natural numbers, but each $A_n$ is itself different. Prove the union is countable.
As an example, you could have the set of all pairs $A_n = {(n, i) : i \in \mathbb{N}}$. Perhaps I can make it simpler and just use that concrete choice in the next version of the book...
Sorry, I was mistaken. The previous exercise already uses that concrete construction. I suppose the point of this exercise was to show that N x N is not special in this regard. I.e., you can take countably infinite sets that don't look like N and give the necessary bijection to N x N
The definition of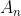 is not clear from the question. I could think of two possible interpretations:
is not clear from the question. I could think of two possible interpretations: 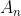 is a set consisting of any
is a set consisting of any 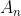 consists of numbers from
consists of numbers from
nnatural numbers, or another interpretation is that1ton.In the latter interpretation, it is pretty straightforward to prove that the union of all such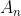 will essentially be
will essentially be

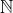
Nwhich has an injective mapping from
In the former case I am confused if it can be shown that there will be a injection from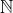 to the union because I can always select arbitrary
to the union because I can always select arbitrary 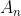 which always excludes certain numbers from
which always excludes certain numbers from 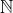 (say none of the
(say none of the 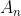 has
has  . In this case it is easy to show a surjection from
. In this case it is easy to show a surjection from 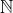 to
to  but will it also be an injection because of the their infinite cardinality?
but will it also be an injection because of the their infinite cardinality?
1) then the union will essentially beThe text was updated successfully, but these errors were encountered: