分类算法
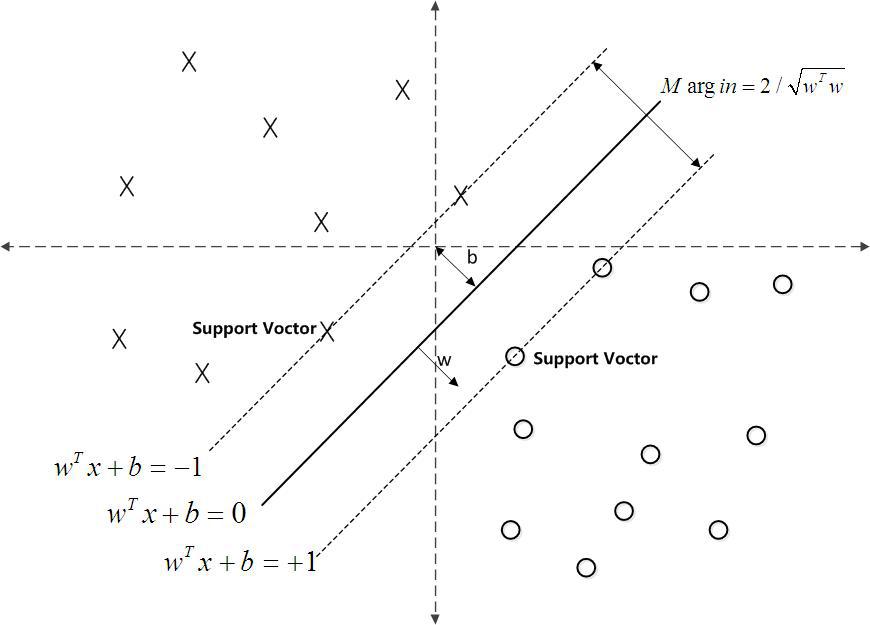
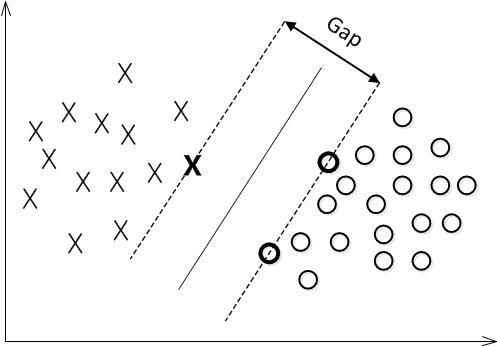
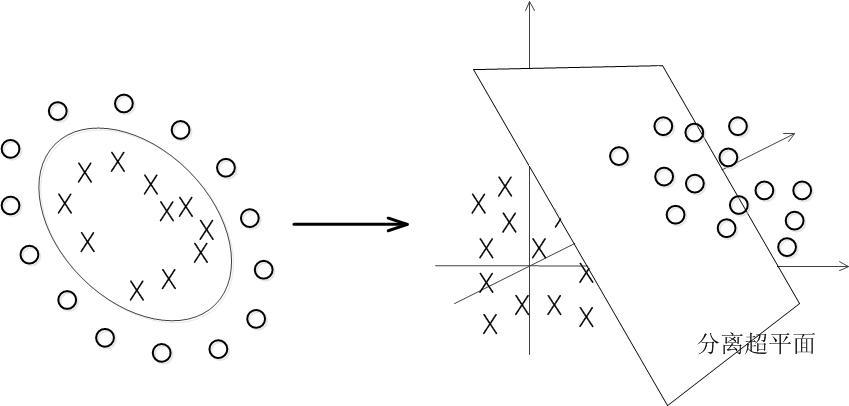
寻找一个超平面
具体做法: 找到离分隔超平面最近的点,确保它们离分隔面的距离尽可能远。
详细公式推导:支持向量机通俗导论(理解SVM的三层境界)
SVM的目标是找到一个可以分割两类的超平面,并使其离数据的间隔(几何间隙)最大。
通过对偶问题,将其转化为一个凸二次优化问题
通过拉格朗日函数将其转化为无约束问题,最终可以转化成下述目标函数:
为使解符合约束条件,就要最大化拉格朗日乘子(Lagrange Multiplier)$\alpha$, 令
故原来的有约束优化问题变为: $$\min _{w, b} \theta(w)=\min _{w, b} \max {\alpha{i} \geq 0} \mathcal{L}(w, b, \alpha)=p^{*}$$
为求解方便,调换顺序,即先对$\omega, b$最小化,再对$\alpha$最大化: $$\max {\alpha{i} \geq 0} \min _{w, b} \mathcal{L}(w, b, \alpha)=d^{*}$$
此处省略KKT条件的证明。
- 让
$\mathcal{L}$ 对$\omega,b$ 最小化,即对它们分别求偏导:
- 化简为只包含拉格朗日乘子的优化问题,再对乘子最大化:
- 利用 SMO 算法求解对偶问题中的拉格朗日乘子。
利用求解对偶问题的序列最小最优化SMO算法计算出拉格朗日因子,再计算出w和b。SMO总结下来就是重复下面的过程:
- 选择两个拉格朗日乘子αi和αj;
- 固定其他拉格朗日乘子αk(k不等于i和j),只对αi和αj优化w(α);
- 根据优化后的αi和αj,更新截距b的值;
def fit(self, X_train, Y_train):
self.kernel_process(X_train, Y_train, self.kernel)
for now_iter in range(self.epoch):
alpha_prev = np.copy(self.alpha)
for j in range(self.m):
# 选择第二个优化的拉格朗日乘子
i = self.random_index(j)
error_i, error_j = self.error_row(i, alpha_prev), self.error_row(j, alpha_prev)
# 检验他们是否满足KKT条件,然后选择违反KKT条件最严重的self.alpha[j]
if (self.Y[j] * error_j < -0.001 and self.alpha[j] < self.C) or (self.Y[j] * error_j > 0.001 and self.alpha[j] > 0):
eta = 2.0 * self.K[i, j] - self.K[i, i] - \
self.K[j, j] # 第j个要优化的拉格朗日乘子,最后需要的
if eta >= 0:
continue
L, H = self.getBounds(i, j)
# 旧的拉格朗日乘子的值
old_alpha_j, old_alpha_i = self.alpha[j], self.alpha[i]
# self.alpha[j]的更新
self.alpha[j] -= (self.Y[j] * (error_i - error_j)) / eta
# 根据约束最后更新拉格朗日乘子self.alpha[j],并且更新self.alpha[j]
self.alpha[j] = self.finalValue(self.alpha[j], H, L)
self.alpha[i] = self.alpha[i] + self.Y[i] * \
self.Y[j] * (old_alpha_j - self.alpha[j])
# 更新偏置值b
b1 = self.b - error_i - self.Y[i] * (self.alpha[i] - old_alpha_j) * self.K[i, i] - \
self.Y[j] * (self.alpha[j] -
old_alpha_j) * self.K[i, j]
b2 = self.b - error_j - self.Y[j] * (self.alpha[j] - old_alpha_j) * self.K[j, j] - \
self.Y[i] * (self.alpha[i] -
old_alpha_i) * self.K[i, j]
if 0 < self.alpha[i] < self.C:
self.b = b1
elif 0 < self.alpha[j] < self.C:
self.b = b2
else:
self.b = 0.5 * (b1 + b2)
# 判断是否收敛(终止)
diff = np.linalg.norm(self.alpha - alpha_prev)
if diff < self.epsilon:
self.final_alpha = np.copy(self.alpha)
break
self.final_alpha = np.copy(self.alpha)