Skip to content

Latest commit

 

History

History
536 lines (411 loc) · 41.9 KB

TDA.md

File metadata and controls

536 lines (411 loc) · 41.9 KB
Raw

Topological Data Analysis

Topological data analysis(TDA) is potential to find better representation of the data specially the shape of data. TDA can visualize the high dimensional data and characterize the intrinsic invariants of the data. It is close to computational geometry, manifold learning and computational topology. It is one kind of descriptive representation learning.

Problems of data analysis share many features with these two fundamental integration tasks: (1) how does one infer high dimensional structure from low dimensional representations; and (2) how does one assemble discrete points into global structure.

As The NIPS 2012 workshop on Algebraic Topology and Machine Learning puts:

Topological methods and machine learning have long enjoyed fruitful interactions as evidenced by popular algorithms like ISOMAP, LLE and Laplacian Eigenmaps which have been borne out of studying point cloud data through the lens of geometry. More recently several researchers have been attempting to also understand the algebraic topological properties of data. Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study and classify topological spaces. The machine learning community thus far has focused almost exclusively on clustering as the main tool for unsupervised data analysis. Clustering however only scratches the surface, and algebraic topological methods aim at extracting much richer topological information from data.

TDA example

Topological Data Analysis as its name shown takes the advantages of topological properties of data, which makes it different from manifold learning or computational geometry.

Why TDA?

One of the key messages around topological data analysis is that data has shape and the shape matters. The shape is always not in the term of probability distribution function or cumulant distribution function. The basic goal of TDA is to apply topology, one of the major branches of mathematics, to develop tools for studying geometric features of data.

Perhaps the most elegant demonstration of the dangers of summary statistics is Anscombe’s Quartet. It’s a group of four datasets that appear to be similar when using typical summary statistics, yet tell four different stories when graphed. Each dataset consists of eleven $(x,y)$ pairs as follows:

As shown above, the shape matters. And the distribution can not tell us all the information the datasets encode.

Specially in high dimensional space, it is not easy to depict the shape of data sets in the term of probability distribution function and it is almost impossible to visualize or graph them without dimension reduction. Capturing all kinds of shape requires different method algebraically.

Topology is and Effective Language to Describe Abstractions of Features from Raw Data.

Shape of Data:

  • Normally defined in terms of a distance metric.
  • Euclidean distance, Hamming, correlation distance, etc.
  • Encodes similarity.
Property
Coordinate Freeness
Deformation Invariance
Compressed Representation

Many of the methods currently being used operate as mechanisms for verifying (or disproving) hypotheses generated by an investigator, and therefore rely on that investigator to formulate good models or hypotheses. For many complex data sets, however, the number of possible hypotheses is very large, and the task of generating useful ones becomes very difficult. In this paper, we will discuss a method that allows exploration of the data, without first having to formulate a query or hypothesis. While most approaches to mining big data focus on pairwise relationships as the fundamental building block1, here we demonstrate the importance of understanding the “shape” of data in order to extract meaningful insights.

The fundamental idea is that topological methods act as a geometric approach to pattern or shape recognition within data. Recognizing shapes (patterns) in data is critical to discovering insights in the data and identifying meaningful sub-groups. Typical shapes which appear in these networks are “loops” (continuous circular segments) and “flares” (long linear segments). We typically use these template patterns in an informal way, then identify interesting groups using these shapes. For example, we might select groups to be the data points in the nodes concentrated at the end of a flare.

Topology Basics

Topology focuses on the invariants with respect to continuous mapping. It pays more attention to the geometrical or discrete properties of the objects such as the number of circles or holes. It is not distance-based as much as differential geometry.

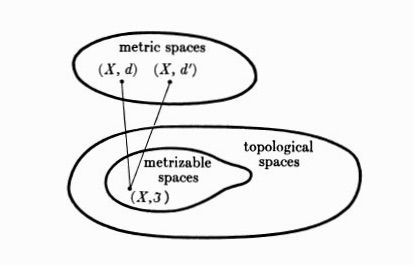
Definition: Let $X$ be a non-empty set. A set $\tau$ of subsets of $X$ is said to be a topology if

  • $X$ and the empty set $\emptyset$ belong to $\tau$;
  • the union of any number of sets in $\tau$ belongs to $\tau$;
  • the intersection of any two sets in $\tau$ belongs to $\tau$.

The pair $(X,\tau)$ is called a topological space.

As the definition shows the topology may be really not based on the definition of distance or measure. The set can be countable or discountable.e3

Definition: Let $(X,\tau)$ be a topological space. Then the members of $\tau$ (the subsets of $X$) is said to be open set. If $X-S$ is open set, we call $S$ as closed set.

From this definition, the open or close set is totally dependent on the set family $\tau$.

Like others in mathematics, the definition of topology is really abstract and strange like the outer space from the eyes of the ordinary living in the earth. Mathematics texts are almostly written in logic order and for the ideal cases. A good piece of news is that topological data analysis does provide many vivid example and concrete application, which does not only consist of mathematical concepts or theorems.

spaces

Definition A topological space $(X, \tau)$ is said to be connected if $X$ is not the union of two disjoint nonempty open sets. Consequently, a topological space is disconnected if the union of any two disjoint nonempty subsets in $\tau$ produces $X$.

Simplices and Simplicial Complexes

Topological data analysis employs the use of simplicial complexes, which are complexes of geometric structures called simplices (singular: simplex). TDA uses simplicial complexes because they can approximate more complicated shapes and are much more mathematically and computationally tractable than the original shapes that they approximate.

Simplices are discrete building blocks for topological spaces.

A simplicial complex is a generalization of a graph, with a few special features. The most particular feature is that simplicial complexes can contain higher order analogs of vertices and edges, referred to as simplices. Simplices can be the familiar vertices and edges of a graph, or triangles drawn between 3 vertices, tetrahedron between 4 vertices, and higher still.

For example, the probability simplex in $\mathbb{R}^n$ is defined as $$\sum_{i=1}^{n}x_i=1,\quad x_i\geq 0\quad \forall i\in{1, 2, \dots, n}.$$

In fact, each component in probability simplex is in the interval $[0, 1]$.

An n-simplex $\sigma$ is the convex hull of $n + 1$ affinely ndependent vertices $S=$ Definition A k-simplex in $X$ is an unordered collection of $k + 1$ distinct elements of $X$.

simplex

Most often, simplicial complexes are built from the nerve of a cover. Intuitively named, a cover of a data set is a collection of subsets of the data such that every data point is in at least one of the subsets. Formally, we say a cover ${U_i}$ of a data set X is satisfies the condition that for any $x \in X$, there exists at least on $U_i \in {U_i}$ such that $x \in U_i$. In practice, we often have that each point is contained in multiple cover elements. The nerve is a simplicial complex created from a cover by collapsing each cover element into vertices and connecting vertices when the cover elements had points in common. If a point was included in two cover elements $U_i$ and $U_j$, then the vertices $\sigma_i, \sigma_j$ would have an edge drawn between them, denoted $\sigma_{ij}$. We continue this process to higher order intersections to create higher order simplices.

The faces of a simplex are its boundaries.

Definition An abstract simplex is any finite set of vertices.

Definition A complex is a collection of multiple simplices.

Definition A simplicial complex $\mathcal {K}$ is a set of simplices that satisfies the following conditions:

  1. Any face of a simplex in $\mathcal {K}$ is also in $\mathcal {K}$.
  2. The intersection of any two simplices $\sigma_{1}, \sigma_{2}\in \mathcal {K}$ is either $\emptyset$ or a face of both $\sigma_{1}$ and $\sigma_{2}$.

Definition (Vietoris-Rips Complex) If we have a set of points $P$ of dimension $d$, and $P$ is a subset of $R^d$, then the Vietoris-Rips (VR) complex $V_{\epsilon}(P)$ at scale $\epsilon$ (the VR complex over the point cloud $P$ with parameter $\epsilon$) is defined as: $$ V_{\epsilon}(P) = {\sigma\subset P\mid d(u, v)\leq \epsilon,\forall u≠v\in\sigma} $$

These VR complexes have been used as a way of associating a simplicial complex to point cloud data sets.

  1. Flag/clique complexes : Given a graph (network) $X$, the flag complex or clique complex of $X$ is the maximal simplicial complex $X$ that has the graph as its 1-skeleton: $X^{(1)}=X$.

  2. Banner Complexes: From flag complexes to banner complexes

  3. Nerve Complexes: Nerves Let $X$ be a topological space and $U = {U_{\alpha}}{\alpha\in A}$ a covering of $X$. The nerve of $U$, denoted $N(U)$, is the abstract simplicial complex with vertex set $A$ and where ${\alpha_0, \cdots , \alpha_k }$ spans a k-simplex if and only if $$U{\alpha_0}\cap\cdots\cap U_{\alpha_k}\not=\emptyset.$$

  4. Dowker Complexes: For simplicity, let $X$ and $Y$ be finite sets with #R \subset X\times Y$ representing the ones in a binary matrix (also denoted R) whose columns are indexed by $X$ and whose rows are indexed by $Y$. The Dowker complex of $R$ on $X$ is the simplicial complex on the vertex set $X$ defined by the rows of the matrix $R$. That is, each row of $R$ determines a subset of $X$: use these to generate a simplex and all its faces. Doing so for all the rows gives the Dowker complex on $X$. There is a dual Dowker complex on $Y$ whose simplices on the vertex set $Y$ are determined by the ones in columns of $R$.

  5. Cell Complexes: Cell Complexes: Definitions

https://ncatlab.org/nlab/show/CW+complex

Nerve Theorem $X$ and $U$ as above, $U$ a covering by open sets which is enumerable. Suppose further that for all $\emptyset \not= S \subset A$ we have that $\cap_{s\in S} U_s$ is either empty or contractible. Then $N(U)$ is homotopy equivalent to $X$.

Definition A family $\Delta$ of non-empty finite subsets of a set $S$ is an abstract simplicial complex if, for every set $X$ in $\Delta$, and every non-empty subset $Y \subset X$, $Y$ also belongs to $\Delta$.

Definition The n-chain, denoted $C_n(S)$ is the subset of an oriented abstract simplicial complex $S$ of n-dimensional simplicies.

Definition The boundary of an n-simplex $X$ with vertex set $[v_0, v_1, v_2,...v_n]$, denoted $\partial(X)$, is: $$\partial(X)=\sum_{i=0}^{n}(−1)^i[v_0, v_1, v_2,...v_n],$$ where the i-th vertex is removed from the sequence.

Betti numbers and Persistence Diagram

Betti numbers and Persistence Diagram (PD) are topological descriptors of a simplicial complex; while Betti numbers count holes of different dimensions, PD tracks the birth and death instances of distinct topological features as the complex is sequentially built piece by piece. Separately, a Minimal Spanning Acycle (MSA) generalizes the notion of a minimal spanning tree to weighted simplicial complexes.

Persistent Homology

Persistent homology (henceforth just PH) gives us a way to find interesting patterns in data without having to "downgrade" the data in anyway so we can see it.

Perhaps the most important idea in applied algebraic topology is persistence. It is a response to the first difficulty that one encounters in attempting to assign topological invariants to statistical data sets: that the topology is not robust and has a sensitive dependence on the length scale at which the data set is being considered. The solution is to calculate the topology (specifically the homology) at all scales simultaneously, and to encode the relationship between the different scales in an algebraic invariant called the persistence diagram.

Persistent homology “generalizes clustering” in two ways: first, that it includes higher-order homological features in addition to the 0th order feature (i.e. the clusters); second, that it includes a persistence parameter that tells us what homological features exist at which scales. One only has to look to the ubiquity of clustering to see that persistent homology is a sensible thing to do.

Robert Ghrist said that

Homology is the simplest, general, computable invariant of topological data. In its most primal manifestation, the homology of a space $X$ returns a sequence of vector spaces $H•(X)$, the dimensions of which count various types of linearly independent holes in $X$. Homology is inherently linear-algebraic, but transcends linear algebra, serving as the inspiration for homological algebra. It is this algebraic engine that powers the subject.

Definition A homotopy between maps, $f_0 \simeq f_1 : X \to Y$ is a continuous 1-parameter family of maps $f_t: X \to Y$. A homotopy equivalence is a map $f : X \to Y$ with a homotopy inverse, $g: Y \to X$ satisfying $f \circ g \simeq {Id}_Y$ and $g \circ f \simeq {Id}_X$.

Greedy optimal homotopy and homology generators Written with Kim Whittlesey HomotopySmall

Euler Characteristic

TDA

Topological data analysis as one data processing method is selected topic for some students on computer science and applied mathematics. It is not popular for the statisticians, where there is no estimation and test.

Topological data analysis (TDA) refers to statistical methods that find structure in data. As the name suggests, these methods make use of topological ideas. Often, the term TDA is used narrowly to describe a particular method called persistent homology.

TDA, which originates from mathematical topology, is a discipline that studies shape. It’s concerned with measuring the shape, by means applying math functions to data, and with representing it in forms of topological networks or combinatorial graphs.

Topological data analysis is more fundamental than revolutionary: such methods are not intended to supplant analytic, probabilistic, or spectral techniques. They can however reveal a deeper basis for why some data sets and systems behave the way they do. It is unwise to wield topological techniques in isolation, assuming that the weapons of unfamiliar "higher" mathematics are clad in incorruptible silver

There is another field that deals with the topological and geometric structure of data: computational geometry. The main difference is that in TDA we treat the data as random points, whereas in computational geometry the data are usually seen as fixed.

tda

TDA can be applied to manifold estimation, nonlinear dimension reduction, mode estimation, ridge estimation and persistent homology.

Persistence-Way

Topological analysis using persistent homology

  • Finds topological invariants in data (# of connected components, enclosed voids, etc.)
  • Input: a (density) function, $f$
  • Output: topological structures & their persistence
  • Def: given threshold $t$, the superlevel set $f^{-1}(t)={x\mid f(x)\geq t}$.
    • the true structures are hidden in superlevel sets
    • consider the whole stack of superlevel sets
    • identify structures that often appear (high persistence)
    • Output: persistence diagram – dots representing all structures

It is beneficial to encode the persistent homology of a data set in the form of a parameterized version of a Betti number: a barcode.

TDA Mapper

The key insight offered by this technique is that many interesting “clusters” in real data are not clusters in the classical sense (as disconnected components), but are the branches of some single connected component. Think about the three “clusters” in the shape $Y$. As simple as this sounds, this insight has been driving real progress in cancer genomics (where the “clusters” are rarely true clusters), and I suspect this method (or some reinvention of it) will find its ways into more fields in due time.

  • Apply a filter function to project data onto a lower dimensional space
  • Performs partial clustering in the level sets

Mapper is an important tool used in TDA for data visualization.

  • Input
    • point cloud;
    • “filter function;”
    • covering of a metric space;
    • clustering algorithm;
    • various other parameters.
  • Output
    • Graph (or higher simplicial complex) which is thought to capture aspects of the topology of the point cloud.

Mapper gives a multi-resolution, low dimensional picture of the point cloud. It’s highly customizable, and has a track record of revealing structure that clustering and (linear or nonlinear) “projection pursuit” methods miss.

Density Cluster with TDA

Resource

Dr Vitaliy Kurlin Applied Algebraic Topology (AAT) network in the UK

Wang Bei was a PI of DBI: ABI Innovation: A Scalable Framework for Visual Exploration and Hypotheses Extraction of Phenomics Data using Topological Analytics.

Wang Bei

giotto-learn

giotto-learn is a high performance topological machine learning toolbox in Python built on top of scikit-learn and is distributed under the Apache 2.0 license. It is part of the Giotto open-source project.

Application

Computational Topology

Computational topology is the mathematical theoretic foundation of topological data analysis. It is different from the deep neural network that origins from the engineering or the simulation to biological neural network. Topological data analysis is principle-driven and application-inspired in some sense.

CS 598: Computational Topology Spring 2013 covers the following topics:

Potential mathematical topics include the topology of cell complexes, topological graph theory, homotopy, covering spaces, simplicial homology, persistent homology, discrete Morse theory, discrete differential geometry, and normal surface theory. Potential computing topics include algorithms for computing topological invariants, graphics and geometry processing, mesh generation, curve and surface reconstruction, VLSI routing, motion planning, manifold learning, clustering, image processing, and combinatorial optimization.

Computational Geometry

https://shapeofdata.wordpress.com/

Computational geometry uses some information of samples or local information of the geometrical objects to reconstruct/describe the whole object. In computer vision, the task 3D reconstruction is a typical example of computational geometry.

discrete differential geomety

Geometric Data Analysis

http://cs233.stanford.ed https://tgda.osu.edu/

Geometric Data Analysis and topological data analysis are out of the mainstream of quantitative statistics while the quantity also matters in geometric data analysis. In conventional statistics, the core concepts are distribution (count in brief) and in/dependence, which is regarded as the reverse engineer of the probability theory. It is supposed that the data is embedded in some "flat" subspace in $\mathbb{R}^n$ in the past. Statistics on Manifold and geometry information extends statistics into higher geometrical level.

Optimal Transport