Skip to content

Latest commit

 

History

History
1875 lines (1518 loc) · 135 KB

Science of Deep Learning.md

File metadata and controls

1875 lines (1518 loc) · 135 KB
Raw

Science of Learning

V. Vapnik said that ``Nothing is more practical than a good theory.'' Here we focus on the theoretical machine learning.

Deep learning is a transformative technology that has delivered impressive improvements in image classification and speech recognition. Many researchers are trying to better understand how to improve prediction performance and also how to improve training methods. Some researchers use experimental techniques; others use theoretical approaches.

There has been a lot of interest in algorithms that learn feature hierarchies from unlabeled data. Deep learning methods such as deep belief networks, sparse coding-based methods, convolutional networks, and deep Boltzmann machines, have shown promise and have already been successfully applied to a variety of tasks in computer vision, audio processing, natural language rocessing, information retrieval, and robotics. In this workshop, we will bring together researchers who are interested in deep learning and unsupervised feature learning, review the recent technical progress, discuss the challenges, and identify promising future research directions.

The development of a "Science of Deep Learning" is now an active, interdisciplinary area of research combining insights from information theory, statistical physics, mathematical biology, and others. Deep learning is at least related with kernel tricks, projection pursuit and neural networks.

Resource on Deep Learning Theory

Blogs and Paper

Course on Deep Learning

Deep Learning Reading Group

yanjun organized a wonderful reading group on deep learning.

Workshops

Labs

Interpretability in AI

Interpretability of Neural Networks

Although deep neural networks have exhibited superior performance in various tasks, interpretability is always Achilles’ heel of deep neural networks. At present, deep neural networks obtain high discrimination power at the cost of a low interpretability of their black-box representations. We believe that high model interpretability may help people break several bottlenecks of deep learning, e.g., learning from a few annotations, learning via human–computer communications at the semantic level, and semantically debugging network representations. We focus on convolutional neural networks (CNNs), and revisit the visualization of CNN representations, methods of diagnosing representations of pre-trained CNNs, approaches for disentangling pre-trained CNN representations, learning of CNNs with disentangled representations, and middle-to-end learning based on model interpretability. Finally, we discuss prospective trends in explainable artificial intelligence.

Not all one can understand the relative theory or quantum theory.

DeepLEVER

DeepLEVER aims at explaining and verifying machine learning systems via combinatorial optimization in general and SAT in particular. The main thesis of the DeepLever project is that a solution to address the challenges faced by ML models is at the intersection of formal methods (FM) and AI. (A recent Summit on Machine Learning Meets Formal Methods offered supporting evidence to how strategic this topic is.) The DeepLever project envisions two main lines of research, concretely explanation and verification of deep ML models, supported by existing and novel constraint reasoning technologies.

DLphi

Together with the participants of the Oberwolfach Seminar: Mathematics of Deep Learning, I wrote a (not entirely serious) paper called "The Oracle of DLPhi" proving that Deep Learning techniques can perform accurate classifications on test data that is entirely uncorrelated to the training data. This, however, requires a couple of non-standard assumptions such as uncountably many data points and the axiom of choice. In a sense this shows that mathematical results on machine learning need to be approached with a bit of scepticism.

Scientific Machine Learning

Scientific machine learning is a burgeoning discipline which blends scientific computing and machine learning. Traditionally, scientific computing focuses on large-scale mechanistic models, usually differential equations, that are derived from scientific laws that simplified and explained phenomena. On the other hand, machine learning focuses on developing non-mechanistic data-driven models which require minimal knowledge and prior assumptions. The two sides have their pros and cons: differential equation models are great at extrapolating, the terms are explainable, and they can be fit with small data and few parameters. Machine learning models on the other hand require "big data" and lots of parameters but are not biased by the scientists ability to correctly identify valid laws and assumptions.

Physics and Deep Learning

Neuronal networks have enjoyed a resurgence both in the worlds of neuroscience, where they yield mathematical frameworks for thinking about complex neural datasets, and in machine learning, where they achieve state of the art results on a variety of tasks, including machine vision, speech recognition, and language translation.
Despite their empirical success, a mathematical theory of how deep neural circuits, with many layers of cascaded nonlinearities, learn and compute remains elusive.
We will discuss three recent vignettes in which ideas from statistical physics can shed light on this issue.
In particular, we show how dynamical criticality can help in neural learning, how the non-intuitive geometry of high dimensional error landscapes can be exploited to speed up learning, and how modern ideas from non-equilibrium statistical physics, like the Jarzynski equality, can be extended to yield powerful algorithms for modeling complex probability distributions.
Time permitting, we will also discuss the relationship between neural network learning dynamics and the developmental time course of semantic concepts in infants.

In recent years, artificial intelligence has made remarkable advancements, impacting many industrial sectors dependent on complex decision-making and optimization. Physics-leaning disciplines also face hard inference problems in complex systems: climate prediction, density matrix estimation for many-body quantum systems, material phase detection, protein-fold quality prediction, parametrization of effective models of high-dimensional neural activity, energy landscapes of transcription factor-binding, etc. Methods using artificial intelligence have in fact already advanced progress on such problems. So, the question is not whether, but how AI serves as a powerful tool for data analysis in academic research, and physics-leaning disciplines in particular.

Machine Learning for Physics

Deep Learning for Physics

Physics for Machine Learning

Physics Informed Machine Learning

Physics Informed Deep Learning

Statistical Mechanics and Deep Learning

The recent striking success of deep neural networks in machine learning raises profound questions about the theoretical principles underlying their success. For example, what can such deep networks compute? How can we train them? How does information propagate through them? Why can they generalize? And how can we teach them to imagine? We review recent work in which methods of physical analysis rooted in statistical mechanics have begun to shed conceptual insights into these questions. These insights yield connections between deep learning and diverse physical and mathematical topics, including random landscapes, spin glasses, jamming, dynamical phase transitions, chaos, Riemannian geometry, random matrix theory, free probability, and nonequilibrium statistical mechanics. Indeed, the fields of statistical mechanics and machine learning have long enjoyed a rich history of strongly coupled interactions, and recent advances at the intersection of statistical mechanics and deep learning suggest these interactions will only deepen going forward.

Born Machine

Born machine is a Probabilistic Generative Modeling.

Quantum Machine learning

Quantum Machine Learning: What Quantum Computing Means to Data Mining explains the most relevant concepts of machine learning, quantum mechanics, and quantum information theory, and contrasts classical learning algorithms to their quantum counterparts.

Tensor network

Tensor network methods are taking a central role in modern quantum physics and beyond. They can provide an efficient approximation to certain classes of quantum states, and the associated graphical language makes it easy to describe and pictorially reason about quantum circuits, channels, protocols, open systems and more. Our goal is to explain tensor networks and some associated methods as quickly and as painlessly as possible. Beginning with the key definitions, the graphical tensor network language is presented through examples. We then provide an introduction to matrix product states. We conclude the tutorial with tensor contractions evaluating combinatorial counting problems. The first one counts the number of solutions for Boolean formulae, whereas the second is Penrose's tensor contraction algorithm, returning the number of 3-edge-colorings of 3-regular planar graphs.

Deep Neural Network and Renormalization Group

Mathematics of Deep Learning

A mathematical theory of deep networks and of why they work as well as they do is now emerging. I will review some recent theoretical results on the approximation power of deep networks including conditions under which they can be exponentially better than shallow learning. A class of deep convolutional networks represent an important special case of these conditions, though weight sharing is not the main reason for their exponential advantage. I will also discuss another puzzle around deep networks: what guarantees that they generalize and they do not overfit despite the number of weights being larger than the number of training data and despite the absence of explicit regularization in the optimization?

Deep Neural Networks and Partial Differential Equations: Approximation Theory and Structural Properties Philipp Petersen, University of Oxford

Discrete Mathematics and Neural Networks

MIP and Deep Learning

Numerical Analysis for Deep Learning

Dynamics of deep learning is to consider deep learning as a dynamic system. For example, the forward feedback network is expressed in the recurrent form: $$x^{t+1} = f_t(x^{t}),t\in [0,1,\cdots, T]$$ where $f_t$ is some nonlinear function and $t$ is discrete.

However, it is not easy to select a proper nonlinear function $f_t ,,\forall t\in[0,1,\cdots, T]$ and the number $T$. In another word, there are no unified scientific principle or guide to design the structure of deep neural network models.

Many recursive formula share the same feedback forms or hidden structure, where the next input is the output of previous or historical record or generated points.

ResNets

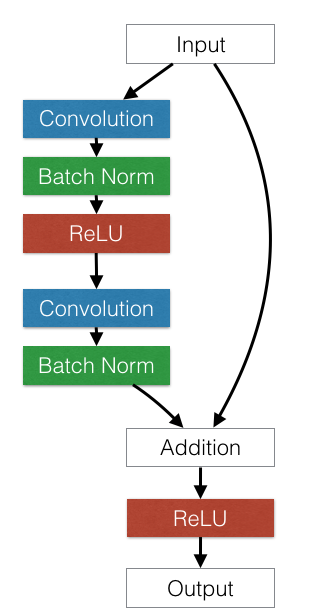
Deep Residual Networks won the 1st places in: ImageNet classification, ImageNet detection, ImageNet localization, COCO detection, and COCO segmentation. It inspired more efficient forward convolutional networks.

They take a standard feed-forward ConvNet and add skip connections that bypass (or shortcut) a few convolution layers at a time. Each bypass gives rise to a residual block in which the convolution layers predict a residual that is added to the block’s input tensor.

Reversible Residual Network

Differential Equations Motivated Deep Learning Methods

This section is on insight from numerical analysis to inspire more effective deep learning architecture.

Many effective networks can be interpreted as different numerical discretizations of differential equations. This finding brings us a brand new perspective on the design of effective deep architectures.

We show that residual neural networks can be interpreted as discretizations of a nonlinear time-dependent ordinary differential equation that depends on unknown parameters, i.e., the network weights. We show how this insight has been used, e.g., to study the stability of neural networks, design new architectures, or use established methods from optimal control methods for training ResNets. Finally, we discuss open questions and opportunities for mathematical advances in this area.

Residual networks as discretizations of dynamic systems: $$ Y_1 = Y_0 +h \sigma(K_0 Y_0 + b_0)\ \vdots \ Y_N = Y_{N-1} +h \sigma(K_{N-1} Y_{N-1} + b_{N-1}) $$

This is nothing but a forward Euler discretization of the Ordinary Differential Equation (ODE): $$\partial Y(t)=\sigma(K(t) Y(t) + b(t)), Y(0)=Y_0, t\in[0, T].$$

The goal is to plan a path (via $K$ and $b$) such that the initial data can be linearly separated.

Another idea is to ensure stability by design / constraints on $\sigma$ and $K(t), b(t)$.

ResNet with antisymmetric transformation matrix: $$\partial Y(t)=\sigma([K(t)-K(t)^T] Y(t) + b(t)), Y(0)=Y_0, t\in[0, T].$$

Hamiltonian-like ResNet $$\frac{\mathrm d}{\mathrm d t}(Y(t), Z(t))^T=\sigma[(K(t)Z(t), -K(t)^T Y(t))^T + b(t)], t\in[0, T].$$

Parabolic Residual Neural Networks

$$\partial Y(t)=\sigma(K(t) Y(t) + b(t)), Y(0)=Y_0, t\in[0, T].$$

Hyperbolic Residual Neural Networks

$$\partial Y(t)=\sigma(K(t) Y(t) + b(t)), Y(0)=Y_0, t\in[0, T].$$

Hamiltonian CNN

$$\partial Y(t)=\sigma(K(t) Y(t) + b(t)), Y(0)=Y_0, t\in[0, T].$$

Numerical differential equation inspired networks: $$Y_{t+1} = (1-k_t)Y_{t-1} + k_t Y_t + h \sigma(K_{t} Y_{t} + b_{t})\tag{Linear multi-step structure}.$$

MgNet

As the solution space is often the dual of the data space in PDEs, the analogous concept of feature space and data space (which are dual to each other) is introduced in CNN. With such connections and new concept in the unified model, the function of various convolution operations and pooling used in CNN can be better understood.

Control Theory and Deep Learning

It arose out of control theory literature when people were trying to identify highly complex and nonlinear dynamical systems. Neural networks – artificial neural networks – were first used in a supervised learning scenario in control theory. Hornik, if I remember correctly, was the first to find that neural networks were universal approximators.

Supervised Deep Learning Problem Given training data, $Y_0$, and labels, $C$, find network parameters $\theta$ and classification weights $W, \mu$ such that the DNN predicts the data-label relationship (and generalizes to new data), i.e., solve $$\operatorname{minimize}_{ \theta,W,\mu} loss[g(W, \mu), C] + regularizer[\theta,W,\mu]$$

This can rewrite in a compact form $$\operatorname{minimize}_{ \theta,W,\mu} loss[g(W(T)Y(T)+\mu), C] + regularizer[\theta,W,\mu]\ \text{subject to }\partial_t Y(t) = f (Y(t), \theta(t)), Y(0) = Y_0.$$

Neural Ordinary Differential Equations

Neural ODE

Dynamics and Deep Learning

Stability For Neural Networks

Differential Equation and Deep Learning

This section is on how to use deep learning or more general machine learning to solve differential equation numerically.

We derive upper bounds on the complexity of ReLU neural networks approximating the solution maps of parametric partial differential equations. In particular, without any knowledge of its concrete shape, we use the inherent low-dimensionality of the solution manifold to obtain approximation rates which are significantly superior to those provided by classical approximation results. We use this low dimensionality to guarantee the existence of a reduced basis. Then, for a large variety of parametric partial differential equations, we construct neural networks that yield approximations of the parametric maps not suffering from a curse of dimension and essentially only depending on the size of the reduced basis.

Deep Learning for PDEs

$\mathcal H$ matrix and deep learning

In this work we introduce a new multiscale artificial neural network based on the structure of H-matrices. This network generalizes the latter to the nonlinear case by introducing a local deep neural network at each spatial scale. Numerical results indicate that the network is able to efficiently approximate discrete nonlinear maps obtained from discretized nonlinear partial differential equations, such as those arising from nonlinear Schodinger equations and the KohnSham density functional theory.

We aim to build a theoretical foundation for the analysis of deep neural networks to answer questions such as "What are the correct approximation spaces for deep neural networks?", "What is the advantage of deep versus shallow networks?", or "To which extent are deep neural networks able to detect low dimensional structures in high dimensional data?".

Stochastic Differential Equations and Deep Learning

Finite Element Methods and Deep Learning

Approximation Theory for Deep Learning

Universal approximation theory show the expression power of deep neural network of some wide while shallow neural network. The section will extend the approximation to the deep neural network.

We derive fundamental lower bounds on the connectivity and the memory requirements of deep neural networks guaranteeing uniform approximation rates for arbitrary function classes in $L^2(\mathbb R^d)$. In other words, we establish a connection between the complexity of a function class and the complexity of deep neural networks approximating functions from this class to within a prescribed accuracy.

The F-Principle

Understanding the training process of Deep Neural Networks (DNNs) is a fundamental problem in the area of deep learning. The study of the training process from the frequency perspective makes important progress in understanding the strength and weakness of DNN, such as generalization and converging speed etc., which may consist in “a reasonably complete picture about the main reasons behind the success of modern machine learning” (E et al., 2019).

The “Frequency Principle” was first named in the paper (Xu et al., 2018), then (Xu 2018; Xu et al., 2019) use more convincing experiments and a simple theory to demonstrate the university of the Frequency Principle. Bengio's paper (Rahaman et al., 2019) also uses the the simple theory in (Xu 2018; Xu et al., 2019) to understand the mechanism underlying the Frequency Principle for ReLU activation function. Note that the second version of Rahaman et al., (2019) points out this citation clearly but they reorganize this citation to “related works” in the final version. Later, Luo et al., (2019) studies the Frequency Principle in the general setting of deep neural networks and mathematically proves Frequency Principle with the assumption of infinite samples. Zhang et al., (2019) study the Frequency Principle in the NTK regime with finite sample points. Zhang et al., (2019) explicitly shows that the converging speed for each frequency and can accurately predict the learning results.

We aim to develop a theoretical framework on Fourier domain to analyze the Deep Neural Network (DNN) training process and understand the DNN generalization. We exemplified our theoretical results through DNNs fitting 1-d functions and the MNIST dataset.

Spline Theory and Deep Network

Resource

Workshop

Labs and Groups

Inverse Problem and Deep Learning

There is a long history of algorithmic development for solving inverse problems arising in sensing and imaging systems and beyond. Examples include medical and computational imaging, compressive sensing, as well as community detection in networks. Until recently, most algorithms for solving inverse problems in the imaging and network sciences were based on static signal models derived from physics or intuition, such as wavelets or sparse representations.

Today, the best performing approaches for the aforementioned image reconstruction and sensing problems are based on deep learning, which learn various elements of the method including i) signal representations, ii) stepsizes and parameters of iterative algorithms, iii) regularizers, and iv) entire inverse functions. For example, it has recently been shown that solving a variety of inverse problems by transforming an iterative, physics-based algorithm into a deep network whose parameters can be learned from training data, offers faster convergence and/or a better quality solution. Moreover, even with very little or no learning, deep neural networks enable superior performance for classical linear inverse problems such as denoising and compressive sensing. Motivated by those success stories, researchers are redesigning traditional imaging and sensing systems.

Deep Learning for Inverse Problems

Learning-based methods, and in particular deep neural networks, have emerged as highly successful and universal tools for image and signal recovery and restoration. They achieve state-of-the-art results on tasks ranging from image denoising, image compression, and image reconstruction from few and noisy measurements. They are starting to be used in important imaging technologies, for example in GEs newest computational tomography scanners and in the newest generation of the iPhone.

The field has a range of theoretical and practical questions that remain unanswered. In particular, learning and neural network-based approaches often lack the guarantees of traditional physics-based methods. Further, while superior on average, learning-based methods can make drastic reconstruction errors, such as hallucinating a tumor in an MRI reconstruction or turning a pixelated picture of Obama into a white male.

Deep Inverse Optimization

Random Matrix Theory and Deep Learning

Random matrix focus on the matrix, whose entities are sampled from some specific probability distribution. Weight matrices in deep neural network are initialed in random. However, the model is over-parameterized and it is hard to verify the role of one individual parameter.

Nonlinear Random Matrix Theory

Deep learning and Optimal Transport

Optimal transport (OT) provides a powerful and flexible way to compare probability measures, of all shapes: absolutely continuous, degenerate, or discrete. This includes of course point clouds, histograms of features, and more generally datasets, parametric densities or generative models. Originally proposed by Monge in the eighteenth century, this theory later led to Nobel Prizes for Koopmans and Kantorovich as well as Villani’s Fields Medal in 2010.

Generative Models and Optimal Transport

Geometric Analysis Approach to AI

Why and how that deep learning works well on different tasks remains a mystery from a theoretical perspective. In this paper we draw a geometric picture of the deep learning system by finding its analogies with two existing geometric structures, the geometry of quantum computations and the geometry of the diffeomorphic template matching. In this framework, we give the geometric structures of different deep learning systems including convolutional neural networks, residual networks, recursive neural networks, recurrent neural networks and the equilibrium prapagation framework. We can also analysis the relationship between the geometrical structures and their performance of different networks in an algorithmic level so that the geometric framework may guide the design of the structures and algorithms of deep learning systems.

Loss Surface Of Deep Networks

Tropical Geometry of Deep Neural Networks

The basic idea of tropical geometry is to study the same kinds of questions as in standard algebraic geometry, but change what we mean when we talk about ‘polynomial equations’.

Topology and Deep Learning

We perform topological data analysis on the internal states of convolutional deep neural networks to develop an understanding of the computations that they perform. We apply this understanding to modify the computations so as to (a) speed up computations and (b) improve generalization from one data set of digits to another. One byproduct of the analysis is the production of a geometry on new sets of features on data sets of images, and use this observation to develop a methodology for constructing analogues of CNN's for many other geometries, including the graph structures constructed by topological data analysis.

Topological machine learning

Topology Optimization and Deep Learning

Deep Learning with Topological Data Analysis

Deep Learning with Topological Layer

Topological Layer is used to extract the feature via topological data analysis.

Topological Graph Neural Networks

Topology-Based Graph Classification

Algebra and Deep Learning

Except the matrix and tensor decomposotion for accelerating the deep neural network, Tensor network is close to deep learning model.

Group Equivariant Convolutional Networks

Complex Valued Neural Networks

Aizenberg, Ivaskiv, Pospelov and Hudiakov (1971) (former Soviet Union) proposed a complex-valued neuron model for the first time, and although it was only available in Russian literature, their work can now be read in English (Aizenberg, Aizenberg & Vandewalle, 2000). Prior to that time, most researchers other than Russians had assumed that the first persons to propose a complex-valued neuron were Widrow, McCool and Ball (1975). Interest in the field of neural networks started to grow around 1990, and various types of complex-valued neural network models were subsequently proposed. Since then, their characteristics have been researched, making it possible to solve some problems which could not be solved with the real-valued neuron, and to solve many complicated problems more simply and efficiently.

The complex-valued Neural Network is an extension of a (usual) real-valued neural network, whose input and output signals and parameters such as weights and thresholds are all complex numbers (the activation function is inevitably a complex-valued function).

Quaternion Neural Networks

It looks like Deep (Convolutional) Neural Networks are really powerful. However, there are situations where they don’t deliver as expected. I assume that perhaps many are happy with pre-trained VGG, Resnet, YOLO, SqueezeNext, MobileNet, etc. models because they are “good enough”, even though they break quite easily on really realistic problems and require tons of training data. IMHO there are much smarter approaches out there, which are neglected/ignored. I don’t want to argue why they are ignored but I want to provide a list with other useful architectures.

Instead of staying with real numbers, we should have a look at complex numbers as well. Let’s remember the single reason why we use complex numbers ($C$) or quaternions ($\mathcal H$). The most important reason why we use complex numbers is not to solve $x^2=−1$. The reason why we use complex numbers for everything that involves waves etc. is that we are lazy or efficient ;). Who wants to waste time writing down and solving a bunch of trignometric identities. The same is true for quaternions in robotics. Speaking in terms of computer science, we are using a much more efficient data structure/representation. It seems like complex valued neural networks as well as quaternion, which are a different kind of complex numbers for the mathematical correct reader of this post, seem to outperform real valued neural networks while using less parameters. This makes sense because we are using a different data structure that itself helps to represent certain things in a much more useful way.

Probabilistic Theory and Deep Learning

Probabilistic Deep Learning

Probabilistic Deep Learning with Python teaches the increasingly popular probabilistic approach to deep learning that allows you to tune and refine your results more quickly and accurately without as much trial-and-error testing. Emphasizing practical techniques that use the Python-based Tensorflow Probability Framework, you’ll learn to build highly-performant deep learning applications that can reliably handle the noise and uncertainty of real-world data.

Bayesian Deep Learning

The abstract of Bayesian Deep learning put that:

While deep learning has been revolutionary for machine learning, most modern deep learning models cannot represent their uncertainty nor take advantage of the well studied tools of probability theory. This has started to change following recent developments of tools and techniques combining Bayesian approaches with deep learning. The intersection of the two fields has received great interest from the community over the past few years, with the introduction of new deep learning models that take advantage of Bayesian techniques, as well as Bayesian models that incorporate deep learning elements [1-11]. In fact, the use of Bayesian techniques in deep learning can be traced back to the 1990s’, in seminal works by Radford Neal [12], David MacKay [13], and Dayan et al. [14]. These gave us tools to reason about deep models’ confidence, and achieved state-of-the-art performance on many tasks. However earlier tools did not adapt when new needs arose (such as scalability to big data), and were consequently forgotten. Such ideas are now being revisited in light of new advances in the field, yielding many exciting new results Extending on last year’s workshop’s success, this workshop will again study the advantages and disadvantages of such ideas, and will be a platform to host the recent flourish of ideas using Bayesian approaches in deep learning and using deep learning tools in Bayesian modelling. The program includes a mix of invited talks, contributed talks, and contributed posters. It will be composed of five themes: deep generative models, variational inference using neural network recognition models, practical approximate inference techniques in Bayesian neural networks, applications of Bayesian neural networks, and information theory in deep learning. Future directions for the field will be debated in a panel discussion. This year’s main theme will focus on applications of Bayesian deep learning within machine learning and outside of it.

  1. Kingma, DP and Welling, M, "Auto-encoding variational Bayes", 2013.
  2. Rezende, D, Mohamed, S, and Wierstra, D, "Stochastic backpropagation and approximate inference in deep generative models", 2014.
  3. Blundell, C, Cornebise, J, Kavukcuoglu, K, and Wierstra, D, "Weight uncertainty in neural network", 2015.
  4. Hernandez-Lobato, JM and Adams, R, "Probabilistic backpropagation for scalable learning of Bayesian neural networks", 2015.
  5. Gal, Y and Ghahramani, Z, "Dropout as a Bayesian approximation: Representing model uncertainty in deep learning", 2015.
  6. Gal, Y and Ghahramani, G, "Bayesian convolutional neural networks with Bernoulli approximate variational inference", 2015.
  7. Kingma, D, Salimans, T, and Welling, M. "Variational dropout and the local reparameterization trick", 2015.
  8. Balan, AK, Rathod, V, Murphy, KP, and Welling, M, "Bayesian dark knowledge", 2015.
  9. Louizos, C and Welling, M, “Structured and Efficient Variational Deep Learning with Matrix Gaussian Posteriors”, 2016.
  10. Lawrence, ND and Quinonero-Candela, J, “Local distance preservation in the GP-LVM through back constraints”, 2006.
  11. Tran, D, Ranganath, R, and Blei, DM, “Variational Gaussian Process”, 2015.
  12. Neal, R, "Bayesian Learning for Neural Networks", 1996.
  13. MacKay, D, "A practical Bayesian framework for backpropagation networks", 1992.
  14. Dayan, P, Hinton, G, Neal, R, and Zemel, S, "The Helmholtz machine", 1995.
  15. Wilson, AG, Hu, Z, Salakhutdinov, R, and Xing, EP, “Deep Kernel Learning”, 2016.
  16. Saatchi, Y and Wilson, AG, “Bayesian GAN”, 2017.
  17. MacKay, D.J.C. “Bayesian Methods for Adaptive Models”, PhD thesis, 1992.

Statistics and Deep Learning

A History of Deep Learning

Mathematician Ivakhnenko and associates including Lapa arguably created the first working deep learning networks in 1965, applying what had been only theories and ideas up to that point.

Ivakhnenko developed the Group Method of Data Handling (GMDH) – defined as a “family of inductive algorithms for computer-based mathematical modeling of multi-parametric datasets that features fully automatic structural and parametric optimization of models” – and applied it to neural networks.

For that reason alone, many consider Ivakhnenko the father of modern deep learning.

His learning algorithms used deep feedforward multilayer perceptrons using statistical methods at each layer to find the best features and forward them through the system.

Using GMDH, Ivakhnenko was able to create an 8-layer deep network in 1971, and he successfully demonstrated the learning process in a computer identification system called Alpha.

Statistical Relational AI

Handling inherent uncertainty and exploiting compositional structure are fundamental to understanding and designing large-scale systems. Statistical relational learning builds on ideas from probability theory and statistics to address uncertainty while incorporating tools from logic, databases, and programming languages to represent structure. In Introduction to Statistical Relational Learning, leading researchers in this emerging area of machine learning describe current formalisms, models, and algorithms that enable effective and robust reasoning about richly structured systems and data.

Principal Component Neural Networks

Nonlinear principal component analysis (NLPCA) is commonly seen as a nonlinear generalization of standard principal component analysis (PCA). It generalizes the principal components from straight lines to curves (nonlinear). Thus, the subspace in the original data space which is described by all nonlinear components is also curved. Nonlinear PCA can be achieved by using a neural network with an autoassociative architecture also known as autoencoder, replicator network, bottleneck or sandglass type network. Such autoassociative neural network is a multi-layer perceptron that performs an identity mapping, meaning that the output of the network is required to be identical to the input. However, in the middle of the network is a layer that works as a bottleneck in which a reduction of the dimension of the data is enforced. This bottleneck-layer provides the desired component values (scores).

Least squares support vector machines

Information Theory and Deep Learning

In short, Neural Networks extract from the data the most relevant part of the information that describes the statistical dependence between the features and the labels. In other words, the size of a Neural Networks specifies a data structure that we can compute and store, and the result of training the network is the best approximation of the statistical relationship between the features and the labels that can be represented by this data structure.

Universal Feature Selection

In this talk, we formulate a new problem called the "universal feature selection" problem, where we need to select from the high dimensional data a low dimensional feature that can be used to solve, not one, but a family of inference problems. We solve this problem by developing a new information metric that can be used to quantify the semantics of data, and by using a geometric analysis approach. We then show that a number of concepts in information theory and statistics such as the HGR correlation and common information are closely connected to the universal feature selection problem. At the same time, a number of learning algorithms, PCA, Compressed Sensing, FM, deep neural networks, etc., can also be interpreted as implicitly or explicitly solving the same problem, with various forms of constraints.

Information Bottleneck Theory

InfoMax

Deep Learning and Coding Theory

https://ee.stanford.edu/event/seminar/isl-seminar-inventing-algorithms-deep-learning

The first is reliable communication over noisy media where we successfully revisit classical open problems in information theory; we show that creatively trained and architected neural networks can beat state of the art on the AWGN channel with noisy feedback by a 100 fold improvement in bit error rate.

The second is optimization and classification problems on graphs, where the key algorithmic challenge is scalable performance to arbitrary sized graphs. Representing graphs as randomized nonlinear dynamical systems via recurrent neural networks, we show that creative adversarial training allows one to train on small size graphs and test on much larger sized graphs (100~1000x) with approximation ratios that rival state of the art on a variety of optimization problems across the complexity theoretic hardness spectrum.

Communication algorithms via deep learning

Learning-based coded computation

Neural Audio Coding

Neural audio coding is an area where we want to compress an audio signal down to a bitstring, which should be recovered as another audio signal that sounds as similar as possible to human ears, of course, using neural nets. This objective is not that straightforward when it comes to training a neural network that does this autoencoding job, because what I just said in the previous sentence is not well defined as a differentiable loss function.

Brain Science and AI

Artificial intelligence and brain science have had a swinging relationship of convergence and divergence. In the early days of pattern recognition, multi-layer neural networks based on the anatomy and physiology of the visual cortex played a key role, but subsequent sophistication of machine learning promoted methods that are little related to the brain. Recently, however, the remarkable success of deep neural networks in learning from big data has re-evoked the interests in brain-like artificial intelligence.

Neuromorphic Computing

The key challenges in neuromorphic research are matching a human's flexibility, and ability to learn from unstructured stimuli with the energy efficiency of the human brain. The computational building blocks within neuromorphic computing systems are logically analogous to neurons. Spiking neural networks (SNNs) are a novel model for arranging those elements to emulate natural neural networks that exist in biological brains.

Spiking neural networks

SpiNNaker

SpiNNaker is a novel massively-parallel computer architecture, inspired by the fundamental structure and function of the human brain, which itself is composed of billions of simple computing elements, communicating using unreliable spikes.

The project's objectives are two-fold:

  1. To provide a platform for high-performance massively parallel processing appropriate for the simulation of large-scale neural networks in real-time, as a research tool for neuroscientists, computer scientists and roboticists
  2. As an aid in the investigation of new computer architectures, which break the rules of conventional supercomputing, but which we hope will lead to fundamentally new and advantageous principles for energy-efficient massively-parallel computing

SpiNNaker project has delivered the world’s largest neuromorphic computing platform incorporating over a million ARM mobile phone processors and capable of modelling spiking neural networks of the scale of a mouse brain in biological real time

Intel Corporation Loihi and Nx SDK

The Thousand Brains Theory of Intelligence

Numenta has developed a major theory of intelligence and how the brain works called The Thousand Brains Theory of Intelligence, and we’re now exploring how to incorporate key principles of the theory to the field of machine intelligence.

Cognition Science and Deep Learning

Brain science is the physological theorey of cognitive science, which focus on the physical principle of brain function. The core problem of cognition science is how to learn in my eyes.

Artificial deep neural networks (DNNs) initially inspired by the brain enable computers to solve cognitive tasks at which humans excel. In the absence of explanations for such cognitive phenomena, in turn cognitive scientists have started using DNNs as models to investigate biological cognition and its neural basis, creating heated debate.

Predictive coding

Predictive coding is a leading theory of how the brain performs probabilistic inference.

Contrastive Predictive Coding

Hierarchical Predictive Coding

A hierarchical predictive coding model consists of layers of latent variables (tiers). Each tier attempts to predict the adjacent lower tier, resulting in a predicted state and a prediction error. By minimizing the prediction error, both the latent variables and the predictors of these variables are estimated.

This principle is often complemented by more general variations that will be supported in future versions of the package

The lottery ticket hypothesis

The lottery ticket hypothesis proposes that over-parameterization of deep neural networks (DNNs) aids training
by increasing the probability of a “lucky” sub-network initialization being present rather than by helping the optimization process (Frankle & Carbin, 2019).

This project explores the Lottery Ticket Hypothesis: the conjecture that neural networks contain much smaller sparse subnetworks capable of training to full accuracy. In the course of this project, we have demonstrated that these subnetworks existed at initialization in small networks and early in training in larger networks. In addition, we have shown that these lottery ticket subnetworks are state-of-the-art pruned neural networks.

Double Descent

The model with optimal parameters are not equal to the best model. $$\fbox{Learning}\not ={Training} \ Generalization\not ={Optimziation}.$$ Back-propagation (BP), the current de facto training paradigm for deep learning models, is only useful for parameter learning but offers no role in finding an optimal network structure. We need to go beyond BP in order to derive an optimal network, both in structure and in parameter.

We show that the double descent phenomenon occurs in CNNs, ResNets, and transformers: performance first improves, then gets worse, and then improves again with increasing model size, data size, or training time. This effect is often avoided through careful regularization. While this behavior appears to be fairly universal, we don’t yet fully understand why it happens, and view further study of this phenomenon as an important research direction.

Neural Tangents