Skip to content

Latest commit

 

History

History
292 lines (223 loc) · 15.2 KB

Least Squares and Variable Selection.md

File metadata and controls

292 lines (223 loc) · 15.2 KB
Raw

Statistical Foundations of Data Science

Statistical Foundations of Data Science by Jianqing Fan, Runze Li, Cun-Hui Zhang, Hui Zhou discussed advanced latest topics in high dimensional statistics. High-Dimensional Probability: An Introduction with Applications in Data Science is a company to the previous one.

The curse of high dimensionality and the bless of high dimensionality is the core topic of the high dimensional statistics in my belief.

Regression Analysis

New and Evolving Roles of Shrinkage in Large-Scale Prediction and Inference (19w5188)

Regression is a method for studying the relationship between a response variable $Y$ and a covariates $X$. The covariate is also called a predictor variable or a feature.

Regression is not function fitting. In function fitting, it is well-defined - $f(x_i)$ is fixed when $x_i$ is fixed; in regression, it is not always so.

Linear regression is the "hello world" in statistical learning. It is the simplest model to fit the datum. We will induce it in the maximum likelihood estimation perspective. See this link for more information https://www.wikiwand.com/en/Regression_analysis.

Ordinary Least Squares

Representation of Ordinary Least Squares

A linear regression model assumes that the regression function $E(Y|X)$ is linear in the inputs $X_1,\cdots, X_p$. They are simple and often provide an adequate and interpretable description of how the inputs affect the output. Suppose that the datum ${(x_i, y_i)}{i=1}^{n}$, $$ {y}{i} = f({x}{i})+{\epsilon}{i}, $$ where the function $f$ is linear, i.e. $f(x)=w^{T}x + b$. Let $\epsilon = y - f(x)$.Then $\mathbb{E}(\epsilon|X) = \mathbb{E}(y - f(x)|x)=0$ and the residual errors ${{\epsilon}{i}|{\epsilon}{i} = {y}{i} - f(x_i)}{i=1}^{n}$ are i.i.d. in standard Gaussian distribution.

By convention (very important!):

  • $\mathrm{x}$ is assumed to be standardized (mean 0, unit variance);
  • $\mathrm{y}$ is assumed to be centered.

For the linear regression, we could assume $\mathrm{x}$ is in Gaussian distribution.

Evaluation of Ordinary Least Squares

The likelihood of the errors are
$$ L(\epsilon_1,\epsilon_2,\cdots,\epsilon_n)=\prod_{i=1}^{n}\frac{1}{\sqrt{2\pi}}e^{-\epsilon_i^2}. $$

In MLE, we have shown that it is equivalent to $$ \arg\max \prod_{i=1}^{n}\frac{1}{\sqrt{2\pi}}e^{-\epsilon_i^2}=\arg\min\sum_{i=1}^{n}\epsilon_i^2=\arg\min\sum_{i=1}^{n}(y_i-f(x_i))^2. $$

Linear Regression and Likelihood Maximum Estimation
<reliawiki.org>

Optimization of Ordinary Least Squares

For linear regression, the function $f$ is linear, i.e. $f(x) = w^Tx$ where $w$ is the parameters to tune. Thus $\epsilon_i = y_i-w^Tx_i$ and $\sum_{i=1}^{n}(y_i-f(x_i))^2=\sum_{i=1}^{n}(y_i - w^Tx_i)^2$. It is also called residual sum of squares in statistics or objective function in optimization theory. In a compact form, $$ \sum_{i=1}^{n}(y_i - w^T x_i)^2=|Y-Xw|^2,\tag 0, $$

where $Y=(y_1,y_2,\cdots, y_n)^T, X=(x_1, x_2,\cdots,x_n)$. Let the gradient of objective function $|Y-Xw|^2$ be 0, i.e. $$ \nabla_{w}{|Y-Xw|^2}=2X^T(Y-Xw)=0,\tag 1, $$ then we gain that $w=(X^TX)^{-1}X^TY$ if possible.

$\color{lime}{Note}$:

  1. the residual error ${\epsilon_i}_{i=1}^{n}$ are i.i.d. in Gaussian distribution;
  2. the inverse matrix $(X^{T}X)^{-1}$ may not exist in some extreme case.

See more on Wikipedia page.

Ridge Regression and LASSO

When the matrix $X^{T}X$ is not inverse, ordinary least squares does not work. And in ordinary least squares, the parameters $w$ is estimated by MLE rather more general Bayesian estimator.

In the perspective of computation, we would like to consider the regularization technique; In the perspective of Bayesian statistics, we would like to consider more proper prior distribution of the parameters.

Ridge Regression As Regularization

It is to optimize the following objective function with parameter norm penalty $$ PRSS_{\ell_2}=\sum_{i=1}^{n}(y_i-w^Tx_i)^2+\lambda w^{T}w=|Y-Xw|^2+\lambda|w|^2,\tag {Ridge}. $$ It is called penalized residual sum of squares. Taking derivatives, we solve $$ \frac{\partial PRSS_{\ell_2}}{\partial w}=2X^T(Y-Xw)+2\lambda w=0 $$ and we gain that $$ w=(X^{T}X+\lambda I)^{-1}X^{T}Y $$ where it is trackable if $\lambda$ is large enough.

LASSO as Regularization

LASSO is the abbreviation of Least Absolute Shrinkage and Selection Operator.

  1. It is to minimize the following objective function： $$ PRSS_{\ell_1}=\sum_{i=1}^{n}(y_i-w^Tx_i)^2+\lambda{|w|}_{1} =|Y-Xw|^2+\lambda{|w|}_1,\tag {LASSO}. $$

  2. the optimization form: $$ \arg\min_{w}\sum_{i=1}^{n}(y_i-w^Tx_i)^2 \qquad\text{objective function} \ \text{subject to},{|w|}_1 \leq t \qquad\text{constraint}. $$

  3. the selection form: $$ \arg\min_{w}{|w|}1 \qquad \text{objective function} \ \text{subject to},\sum{i=1}^{n}(y_i-w^Tx_i)^2 \leq t \qquad \text{constraint}. $$ where ${|w|}1=\sum{i=1}^{n}|w_i|$ if $w=(w_1,w_2,\cdots, w_n)^{T}$.

LASSO and Ridge Regression
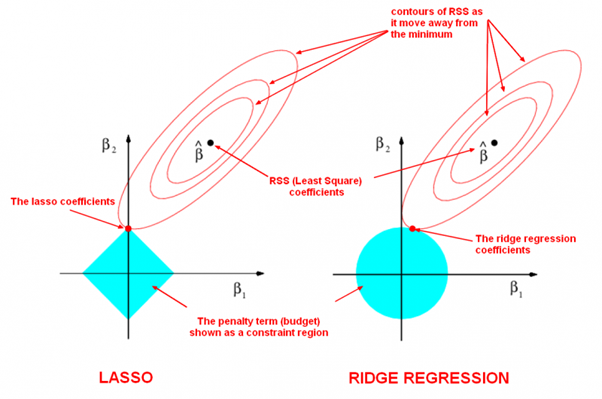The LASSO Page ,Wikipedia page and Q&A in zhihu.com
More References in Chinese blog

Bayesian Perspective

If we suppose the prior distribution of the parameters $w$ is in Gaussian distribution, i.e. $f_{W}(w)\propto e^{-\lambda|w|^{2}}$, we will deduce the ridge regression. If we suppose the prior distribution of the parameters $w$ is in Laplacian distribution, i.e. $f_{W}(w)\propto e^{-\lambda{|w|}_1}$, we will deduce LASSO.

Solution to LASSO: FISTA

Iterative Shrinkage-Threshold Algorithms(ISTA) for $\ell_1$ regularization is $$x^{k+1}=\mathbf{T}{\lambda t}(x^{k}-tA ^{T}(Ax-b))$$ where $t> 0$ is a step size and $\mathbf{T}{\alpha}$ is the shrinkage operator defined by $${\mathbf{T}{\alpha}(x)}{i}={(x_i-\alpha)}{+}sgn(x{i})$$ where $x_i$ is the $i$ th component of $x\in\mathbb{R}^{n}$.

FISTA with constant stepsize

  • $x^{k}= p_{L}(y^k)$ computed as ISTA;
  • $t_{k+1}=\frac{1+\sqrt{1+4t_k^2}}{2}$;
  • $y^{k+1}=x^k+\frac{t_k -1}{t_{k+1}}(x^k-x^{k-1})$.

More solutions to this optimization problem:

Generally, we may consider the penalty residual squared sum $$ PRSS_{\ell_p}=\sum_{i=1}^{n}(y_i -w^T x_i)^2+\lambda{|w|}{p}^{p} =|Y -X w|^2+\lambda{|w|}p^{p},\tag {LASSO} $$ where ${|w|}{p}=(\sum{i=1}^{n}|w_i|^{p})^{1/p}, p\in (0,1)$.

Dr. Zongben Xu proposed the $L_{1/2}$ regularization and its solution.

Elastic Net

When the sample size of training data $n$ is far less than the number of features $p$, the objective function is: $$ PRSS_{\alpha}=\frac{1}{2n}\sum_{i=1}^{n}(y_i -w^T x_i)^2+\lambda\sum_{j=1}^{p}P_{\alpha}(w_j),\tag {Elastic net} $$ where $P_{\alpha}(w_j)=\alpha {|w_j|}_1 + \frac{1}{2}(1-\alpha)(w_j)^2$.

See more on http://web.stanford.edu/~hastie/TALKS/glmnet_webinar.pdf or http://www.princeton.edu/~yc5/ele538_math_data/lectures/model_selection.pdf.

We can deduce it by Bayesian estimation if we suppose the prior distribution of the parameters $w$ is in mixture of Gaussian distribution and Laplacian distribution, i.e. $$f_{W}(w)\propto e^{-\alpha{|w|}_1-\frac{1}{2}(1-\alpha)|w|^{2}}.$$

See Bayesian lasso regression at http://faculty.chicagobooth.edu/workshops/econometrics/past/pdf/asp047v1.pdf.

Sparse Recovery

The nonconvex approach leads to the following optimization problem: $$ \min_{x\in\mathbb{R}^{p}} J(x) = \frac{1}{2}{|Ax-b|}2^2+\sum{i=1}^{p}{\rho}_{\lambda,\tau}(x_i) $$

where ${\rho}{\lambda,\tau}$ is nonconvex penalty, $\lambda>0$ is a regularization parameter and $\tau$ controls the degree of convexity of the penalty. Because the cost function is separable, we will define a thresholding operator $S^{\rho}{\lambda, \tau}$ with respect of the penalty ${\rho}{\lambda,\tau}$: $$S^{\rho}{\lambda, \tau}(v)=\arg\min_{u\in\mathbb{R}^p}{\frac{(u-v)^2}{2}+{\rho}_{\lambda,\tau}(u)}$$

  • LASSO: ${\rho}{\lambda,\tau}=\lambda |t|$, $S{\lambda,\tau}^{\rho}(v) = sgn(v){(|v| -\lambda)}_{+}$;
  • SCAD, $\tau&gt;2$, $$ {\rho}_{\lambda,\tau}(t) = \begin{cases} \lambda |t|, &\text{$|t|\leq\lambda$}\ \frac{\lambda\tau|t|-\frac{1}{2}(t^2+\lambda^2)}{2}, &\text{$\lambda<|t|\leq\lambda\tau$}\ \frac{\lambda^2(\tau +1)}{2}, &\text{$|t|>\lambda\tau$} \end{cases}. $$

$$ S_{\lambda,\tau}^{\rho}(v) = \begin{cases} 0, &\text{$|v|\leq\lambda$}\\ sgn(v)(|v|-\lambda), &\text{$\lambda<|v|\leq 2\lambda$}\\ sgn(v)\frac{(\tau -1)|v|-\lambda\tau}{\tau - 2}, &\text{$2\lambda<|v|\leq \lambda\tau$}\\ v, &\text{$|v|>\lambda\tau$} \end{cases}. $$

  • MCP, $\tau &gt;1$, $$ {\rho}_{\lambda,\tau}(t) = \begin{cases} \lambda (|t|-\frac{t^2}{2\lambda \tau}), &\text{if $|t|&lt;\tau\lambda$} \ \frac{\lambda^2\tau}{2}, &\text{if $|t|\geq \tau\lambda$} \end{cases}. $$

$$ S_{\lambda,\tau}^{\rho}(v) = \begin{cases} 0, &\text{$|v|\leq\lambda$}\\ sgn(v)\frac{(|v|-\lambda)}{\tau - 1}, &\text{$\lambda<|v|\leq \tau\lambda$}\\ v, &\text{$|v|>\lambda\tau$} \end{cases}. $$

Variable Selection: $p\gg N$

In this chapter we discuss prediction problems in which the number of features ${p}$ is much larger than the number of observations ${N}$, often written $p\gg N$. Such problems have become of increasing importance, especially in gnomics and other areas of computational biology.

The outcome ${y}$ was generated according to a linear model of the feature vector $x$: $$ y = \left<w, x\right> +\sigma\epsilon $$

where $w, x\in\mathbb{R}^p$,$\epsilon$ was generated from a standard Gaussian distribution.

Suppose $Y=(y_1, y_2, \dots, y_N)^T\in\mathbb{R}^N$, $X=(x_1, x_2, \dots, x_N)^T\in\mathbb{R}^{P\times N}$, the linear equation system $Y=Xw$ is not posed-well because $p\gg N$. The regularization technique is necessary to solve this question if we do not select some important independent variables. Another question is that colinearity, which makes the features linearly dependent. And what is more, regression is not only optimization. There are more sections on the model selections, explainations or building. More generally, it is one part of the feature engineering - feature selection. Some penalty likelihood functions are proposed to estimate the parameters instead of ordinary likelihood functions in maximum likelihood estimation.