Skip to content

Latest commit

 

History

History
324 lines (246 loc) · 25.9 KB

Back-propagation and beyond.md

File metadata and controls

324 lines (246 loc) · 25.9 KB
Raw

Back-propagation and Beyond

Back-propagation (BP), the current de facto training paradigm for deep learning models, is only useful for parameter learning but offers no role in finding an optimal network structure. We need to go beyond BP in order to derive an optimal network, both in structure and in parameter.

The problem on back-propagation or generally gradient-based training methods of the deep neural networks including the following drawbacks: (1) gradient vanishing or exploring as the fundamental problem of back-propagation; (2) dense computation of gradient; (3) unfriendly for the quantification and without biological plausibility.

Beyond Back-propagation

Training deep learning models does not require gradients such as ADMM, simulated annealing.

Polynomial Neural Networks

The Polynomial Neural Network (PNN) algorithm[1,2] is also known as Iterational Algorithm of Group Methods of Data Handling (GMDH). GMDH were originally proposed by Prof. A.G. Ivakhnenko. PNN correlates input and target variables using (non) linear regression. The PNN models inherit the format of discrete Volterra series and possess universal approximation abilities. Their approximation properties can be explained using the generalized Stone-Weierstrass theorem and the Kolmogorov-Lorentz superposition theorem.

There have been developed several groups of PNN models:

  • high-order multivariate polynomials: including block polynomials and horizontally expanded polynomials;
  • orthogonal polynomials: including polynomials of orthogonal terms, Chebishev polynomials;
  • trigonometric polynomials: using harmonics with non-multiple frequencies;
  • rational polynomials: including polynomial fractions and sigmoidal power series;
  • local basis polynomials: including radial-basis polynomials and piecewise polynomials;
  • fuzzy polynomials: using various membership functions;
  • dynamic polynomials: including time-lagged, NARMA polynomials and recurrent PNN.

In the hope to capture the complexity of a process, the artificial neural networks attempt to decompose it into many simpler relationships each described by a processing function of a single neuron. The processing function of the neurons is quite simple; it is the configuration of the network itself that requires much work to design and adjust to the training data. In 1961, Frank Rosenblatt had identified the key weakness of neurocomputing as the lack of means for effectively selecting structure and weights of the hidden layer(s) of the perceptron. In 1968, when backpropagation technique was not known yet, a technique called Group Method of Data Handling (GMDH) was developed by an Ukranian scientist Aleksey Ivakhnenko who was working at that time on a better prediction of fish population in rivers.

Alternating Projection Neural Networks

Random Projection Neural Networks

Invertible Neural Networks

Beyond Back-propagation

Operator Splitting Methods For Training Deep Neural Networks

ADMM

ADMM is based on the constraints of successive layers in neural networks. Recall the feedforward neural networks: $$O=\sigma(W^N x^{N}+b_{N})\ x^{n}=\sigma(W^{n-1}x^{n-1}+b_{n-1})\quad\forall n=1,\cdots, N $$ The parameters in each layer are updated backward and then forward so that the parameter information in each layer is exchanged efficiently. The time complexity is reduced from cubic to quadratic in (latent) feature dimensions via a dedicated algorithm design for subproblems that enhances them utilizing iterative quadratic approximations and backtracking. Finally, we provide the first proof of global convergence for an ADMM-based method (dlADMM) in a deep neural network problem under mild conditions. Experiments on benchmark datasets demonstrated that our proposed dlADMM algorithm outperforms most of the comparison methods.

Lifted Proximal Operator Machine (LPOM)

By rewriting the activation function as an equivalent proximal operator, we approximate a feed-forward neural network by adding the proximal operators to the objective function as penalties, hence we call the lifted proximal operator machine (LPOM). LPOM is block multi-convex in all layer-wise weights and activations. This allows us to use block coordinate descent to update the layer-wise weights and activations in parallel. Most notably, we only use the mapping of the activation function itself, rather than its derivatives, thus avoiding the gradient vanishing or blow-up issues in gradient based training methods. So our method is applicable to various non-decreasing Lipschitz continuous activation functions, which can be saturating and non-differentiable. LPOM does not require more auxiliary variables than the layer-wise activations, thus using roughly the same amount of memory as stochastic gradient descent (SGD) does. We further prove the convergence of updating the layer-wise weights and activations. Experiments on MNIST and CIFAR-10 datasets testify to the advantages of LPOM.

LPOM is block multi-convex in all layer-wise weights and activations. This allows us to use block coordinate descent to update the layer-wise weights and activations. Most notably, we only use the mapping of the activation function itself, rather than its derivatives, thus avoiding the gradient vanishing or blowup issues in gradient based training methods.

By introducing the layer-wise activations as a block of auxiliary variables, the training of a neural network can be equivalently formulated as an equality constrained optimization problem: $$\min_{W^i, X^i}\ell(X^n, L)\ X^i=\phi(W^{i-1}X^{i-1})$$

where $X^i$ is the activation of the i-th layer, $X^1 \in \mathbb{R}^{n_1\times m}$ is a batch of training samples, $L \in\mathbb{R}^{c\times m}$ denotes the corresponding labels, $n_1$ is the dimension of the training samples, $m$ is the batch size, $c$ is the number of classes, ${W_i}^{n−1}_{i=1}$ are the weights to be learned in which the biases have been omitted for simplicity, $\phi(·)$ is an elementwise activation function (e.g., sigmoid, tanh, and ReLU), and $\ell(\cdot, \cdot)$ is the loss function (e.g., the least-square error or the cross-entropy error).

ANd there are many ways to approxmate this optimization probelm.

Then the optimality condition of the following minimization problem: $$\arg\min_{\textbf{X}^{i}}\textbf{1}^Tf(\textbf{X}^{i})\textbf{1}+\frac{1}{2}|\textbf{X}^{i}-\textbf{W}^{i-1}\textbf{X}^{i-1}|F^2$$ is $$\mathbb{0}\in \phi^{-1}(\textbf{X}^{i})-\textbf{W}^{i-1}\textbf{X}^{i-1}$$ where where $\textbf{1}$ is an all-one column vector; and $\textbf{X}^{i}$ are matrix; $f(x)=\int{0}^{x}(\phi^{-1}(y)-y)\mathrm{d} y$.

So the optimal solution of this condition is $$\textbf{X}^{i}=\phi(\textbf{W}^{i-1}\textbf{X}^{i-1}).$$

And LPOM is to solve the following question:

$$\min_{W^i, X^i}\ell(X^n, L)+\sum_{i=2}^n\mu_i {\textbf{1}^Tf(\textbf{X}^{i})\textbf{1}+\textbf{1}^T g(\textbf{W}^{i-1}\textbf{X}^{i-1})\textbf{1}+\frac{1}{2}|\textbf{X}^{i}-\textbf{W}^{i-1}\textbf{X}^{i-1}|F^2}$$ where $g(x)=\int{0}^{x}(\phi(y)-y)\mathrm{d} y$. It is additively separable

It is shown that the above objective function is block multi-convex.

And we can update the $X^i$ by iterating: $$X^{i, t+1}=\phi(W^{i-1}X^{i-1}-\frac{\mu_{i+1}}{\mu_i}W^{i}(\phi(W^iX^{i, t})-X^{i+1}))$$ and update $X^n$ by iterating $$X^{n, t+1}=\phi(W^{n-1}X^{n-1}-\frac{1}{\mu_n}\frac{\partial \ell(X^{n, t}, L)}{\partial X^n}).$$ We can update the $W^i$ by iterating: $$W^{i, t}=\arg\min_{W}\textbf{1}^T g(\textbf{W}^{i-1}\textbf{X}^{i-1})\textbf{1}+\frac{1}{2}|\textbf{X}^{i}-\textbf{W}^{i-1}\textbf{X}^{i-1}|_F^2.$$

Mixed Integer Optimization

Network models and integer programs are applicable for an enormous known variety of decision problems. Some of these decision problems are really physical problems, such as transportation or flow of commodities. Many network problems are more of an abstract representations of processes or activities, such as the critical path activity network in project management. These problems are easily illustrated by using a network of arcs, and nodes.

Lagrangian Propagator

It has been showed that Neural Networks can be embedded in a Constraint Programming model by simply encoding each neuron as a global constraint, which is then propagated individually. Unfortunately, this decomposition approach may lead to weak bounds.

Layer-wise Relevance Propagation

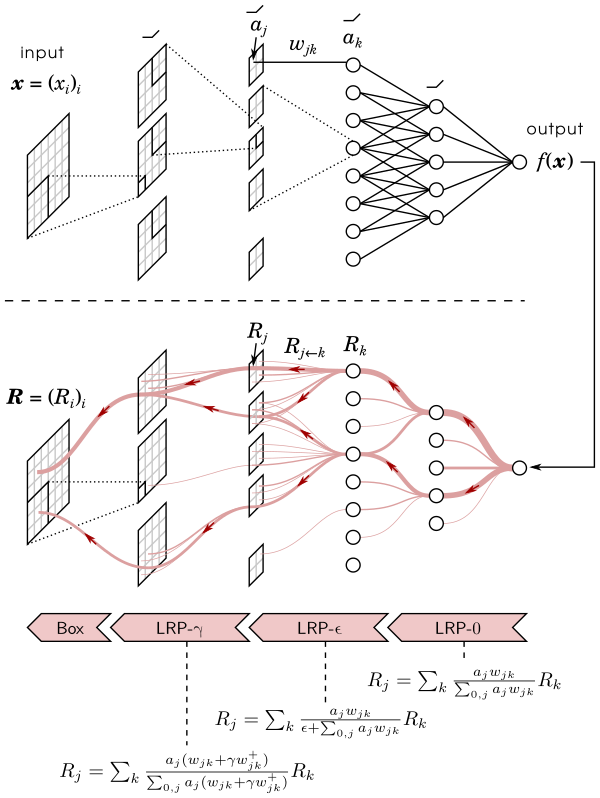
Layer-wise Relevance Propagation (LRP) is a method that identifies important pixels by running a backward pass in the neural network. The backward pass is a conservative relevance redistribution procedure, where neurons that contribute the most to the higher-layer receive most relevance from it. The LRP procedure is shown graphically in the figure below.

Target Propagation

Back-propagation has been the workhorse of recent successes of deep learning but it relies on infinitesimal effects (partial derivatives) in order to perform credit assignment. This could become a serious issue as one considers deeper and more non-linear functions, e.g., consider the extreme case of non-linearity where the relation between parameters and cost is actually discrete. Inspired by the biological implausibility of back-propagation, a few approaches have been proposed in the past that could play a similar credit assignment role as backprop. In this spirit, we explore a novel approach to credit assignment in deep networks that we call target propagation. The main idea is to compute targets rather than gradients, at each layer. Like gradients, they are propagated backwards. In a way that is related but different from previously proposed proxies for back-propagation which rely on a backwards network with symmetric weights, target propagation relies on auto-encoders at each layer. Unlike back-propagation, it can be applied even when units exchange stochastic bits rather than real numbers. We show that a linear correction for the imperfectness of the auto-encoders is very effective to make target propagation actually work, along with adaptive learning rates.

Gradient Target Propagation

We report a learning rule for neural networks that computes how much each neuron should contribute to minimize a giving cost function via the estimation of its target value. By theoretical analysis, we show that this learning rule contains backpropagation, Hebbian learning, and additional terms. We also give a general technique for weights initialization. Our results are at least as good as those obtained with backpropagation.

Dynamic Hierarchical Mimicking

Capsule Networks and More

Capsule Networks provide a way to detect parts of objects in an image and represent spatial relationships between those parts. This means that capsule networks are able to recognize the same object in a variety of different poses even if they have not seen that pose in training data.

Deep Stochastic Configuration Networks

In contrast to known randomized learning algorithms for single layer feed-forward neural networks (e.g., random vector functional-link networks), Stochastic Configuration Networks (SCNs) randomly assign the input weights and biases of the hidden nodes in the light of a supervisory mechanism, while the output weights are analytically evaluated in a constructive or selective manner.

Current experimental results indicate that SCNs outperform other randomized neural networks in terms of required human intervention, selection of the scope of random parameters, and fast learning and generalization. `Deep stochastic configuration networks (DeepSCNs)' have been mathematically proved as universal approximators for continous nonlinear functions defined over compact sets. They can be constructed efficiently (much faster than other deep neural networks) and share many great features, such as learning representation and consistency property between learning and generalization.

This website collect some introductory material on DeepSCNs, most notably a brief selection of publications and some software to get started.

MIND-Net

From the analytical perspective, the ad hoc nature of deep learning renders its success at the mercy of trial-and-errors.
To rectify this problem, we advocate a methodic learning paradigm, MIND-Net, which is computationally efficient in training the networks and yet mathematically feasible to analyze.
MIND-Net hinges upon the use of an effective optimization metric, called Discriminant Information (DI).
It will be used as a surrogate of the popular metrics such as 0-1 loss or prediction accuracy. Mathematically, DI is equivalent or closely related to Gauss’ LSE, Fisher’s FDR, and Shannon’s Mutual Information.
We shall explain why is that higher DI means higher linear separability, i.e. higher DI means that the data are more discriminable. In fact, it can be shown that, both theoretically and empirically, a high DI score usually implies a high prediction accuracy.

To facilitate node/layer ranking, we develop an internal learning paradigm, making a good use of (1) internal teacher labels (ITL); and (2) internal optimization metrics (IOM), i.e. DI, for evaluating hidden layers/nodes. In other words, we have incorporated a notion of Internal Neuron's Learnablility (INL) into the traditional external learning paradigm (i.e. BP) and create a new generation of neural networks, called Explainable Neural Network (XNN). Mathematically, we adopt a new IOM, called discriminant information (DI) which offers an effective metric for ranking the nodes/layer in a network. It can be shown that by simply removing redundant and harmful nodes based on DI tended can greatly enhance the model’s robustness. This allows us to develop a joint parameter/structural gradient-type method for deep compression.